Stay Informed
Follow us on social media accounts to stay up to date with REHVA actualities
|
|
Mateusz BogdanPhD. MSc.CFD, Air Quality and | Edouard WaltherPhD. MSc.Building Physics Advisor, |
To
illustrate the issue, let us consider the trivial case of a building with wind
driven cross-ventilation. The standard Building Energy Simulation (BES) tools
compute the transversal cross-ventilation between to openings a and b at a same height z using the Bernoulli equation:
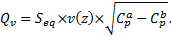
With v(z) is the wind velocity at height z, and Cp is the pressure coefficient on each opposite
façades. The effective opening area Seq is a weighted average of each individual
opening area as well as their respective discharge coefficient, as in the
following equation:
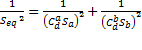 .
.
Sa and Sb represent the actual surface area of both
openings. To overcome Bernoulli hypothesis of non-viscous fluids, their
respective discharge coefficients ![]() and
and ![]() are added. They stand for two distinct
phenomena reducing the theoretical flow. On one hand, the flow vein is
contracting after the opening due to jets inertial effects. The
cross-ventilation is thus reduced by a coefficient Cc, equal to the surface ratio between
the jet area after the opening and the actual opening area (an illustration
presented in Figure 1, for two simplified openings). On
the other hand, the viscous friction also tends to reduce the airflow. It is
usually taken into account through a coefficient Cf, usually taken between 0.95 and
0.99.
are added. They stand for two distinct
phenomena reducing the theoretical flow. On one hand, the flow vein is
contracting after the opening due to jets inertial effects. The
cross-ventilation is thus reduced by a coefficient Cc, equal to the surface ratio between
the jet area after the opening and the actual opening area (an illustration
presented in Figure 1, for two simplified openings). On
the other hand, the viscous friction also tends to reduce the airflow. It is
usually taken into account through a coefficient Cf, usually taken between 0.95 and
0.99.
The discharge coefficient is thus defined by Cc = Cc ´ Cf.
The typical value given in the (ASHRAE 1997) standard and several natural ventilation simulation tools
(CONTAM, IES-VE MacroFlo, EnergyPlus) ranges from 0.60 to 0.65.
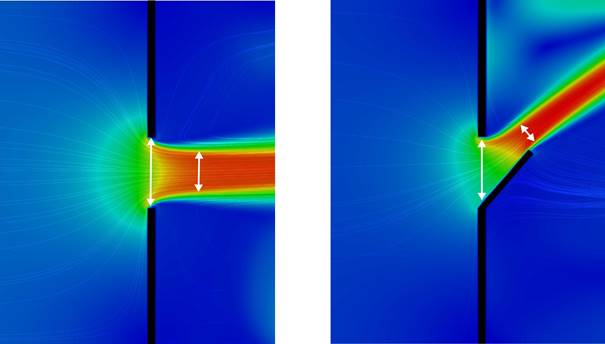
Figure 1. Contraction illustration for two
simplified openings.
Since
neither the stagnation pressure at the opening height, nor at the actual
pressure gap across the two openings a and b are
known in classical BES, a pressure coefficient Cp is introduced for each façade. It
represents a fraction of the undisturbed flow’s dynamic pressure, and can be
either positive or negative, in case of overpressure or depression.
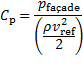
pfaçade![]() represents the stagnation pressure, ρ the air density, and vrefthe wind speed at reference height. According
to the software accuracy, the Cp coefficient is approximated according the
empirical relations, valid only for rectangular buildings, with a shape factor
close to one. Sometimes the inflow angle is also taken into account by a
corrective factor, as well as the building height influence (Swami et Chandra
1988), (Akins, Peterka et Cermak 1979).
represents the stagnation pressure, ρ the air density, and vrefthe wind speed at reference height. According
to the software accuracy, the Cp coefficient is approximated according the
empirical relations, valid only for rectangular buildings, with a shape factor
close to one. Sometimes the inflow angle is also taken into account by a
corrective factor, as well as the building height influence (Swami et Chandra
1988), (Akins, Peterka et Cermak 1979).
The
undisturbed flow velocityvref is taken equal to closest weather
station data. To ascertain the wind speed at the opening height z, a logarithmic law describing the atmospheric boundary layer is used:
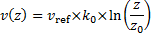
To model
the surroundings of the studied building, the profile of the atmospheric
boundary layer can be adjusted by the terrain constant, the coefficients ko andzo. They
represent respectively the apparent terrain’s roughness and the roughness’
height. ko usually ranges from 0.14 to 0.25, and zo from 0.5 mm to 2 m
according to the terrain (sea, lake, snow field, desert, or at the opposite a
tropical forest or a dense city center).
Reality is
often very different from the theory presented above due to buildings complex
shapes, exact location within an urban context or the actual shapes of
openings. In the following paragraphs, we will demonstrate the possible biases
on each modelling parameter.
Discharge
coefficient:
The Cd coefficient is usually misdocumented by the
manufacturers since it relies on many variables. (Salliou 2011) and (Regard
2000) noted that it may vary according to the opening ratio, the temperature
difference between the inside and outside or the wind speed. In addition, those
authors calculated that this variation ranges from Cd= 0.1 to
Cd= 2, in other word from 10% to 200% influence on the flow
across the opening. However, it is difficult to lift this uncertainty without a
wind tunnel experiment or a numerical simulation. According to the building of
interest, the hypothesis on the Cd should be conservative at best, and the results
should be properly interpreted.
Pressure
coefficient:
Those coefficients vary strongly per the wind direction, its magnitude close to
façades, building shapes and urban surroundings. Even for simple building
geometries, the pressure coefficients are not homogeneous throughout façades. Figure 2
displays a simulation result in terms of Cp, where the values can be contrasted
on a unique façade, ranging from slightly negative to positive values in
certain areas of a same wall.
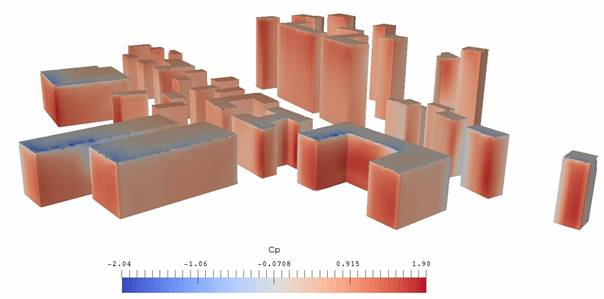
Figure 2.
Façade pressure coefficient unevenness – Chambéry train station urban environment.
Reference
air velocity:
This parameter is taken from the closest weather station, for which the exact
measurement height is usually unknown, nor the precise location. It is hence
often difficult to ascertain precisely the actual wind speed near the location
of interest. The velocity around buildings also depends on the topography, the
close and distant urban settings with their respective roughness’s. Figures 3 & 4 depicts the flows complexity such areas, in plane and sectional view.
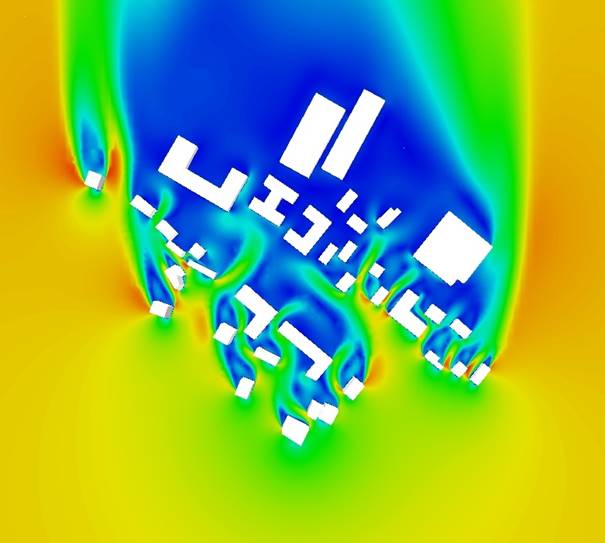
Figure 3. Velocity
field fluctuation in urban environments - plane view.
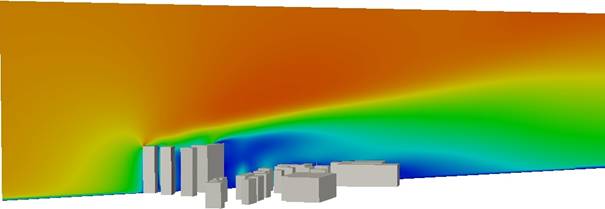
Figure 4.
Velocity field fluctuation in urban areas – sectional view.
The uncertain
parameters reduction should thus be undertaken using computational fluid
dynamics (CFD) simulations. The use of an open-source or purchase-available
software that solve the Reynolds-averaged Navier-Stokes equations coupled to a
mass-balance model (RANS) is then necessary, using for instance a k − e turbulence modelling.
This
approach allows the explicit determination the Cp on each façade of interest,
according to the annual wind data and urban environment. It reduces the
near-building velocities and pressure coefficient uncertainties. Those results
are then taken as inputs for the annual hourly BES. It should nevertheless be
reminded that this approach only considers wind effects: the buoyancy driven
ventilation can be evaluated through a Froude’s numbers condition.
Akins,
R.E., J.A. Peterka, and J.E. Cermak. "Averaged Pressure Coefficients for
Rectangular Buildings." Proceedings of the Fifth International Wind
Engineering Conference. Fort Collins, 1979. 369-380.
ASHRAE.
"Ventilation and Infiltration." In HVAC Fundamentals Handbook,
492-519. Atlanta: ASHRAE Handbook Editor, 1997.
Havenith,
G., I. Holmér, E.A. Den Hartog, and K.C. Parsons. "Clothing Evaporative
Heat Resistance - Proposal for Improved Representation in Standards and
Models." Ann. Occ. Hyg., 1999: (43-5):339-346.
Holmér,
I., H. Nilsson, G. Havenith, and K. Parsons. "Clothing Convective Heat
Exchange -Proposal for Improved Prediction in Standards and Models."
Annals of Occupational Hygiene, 1999: (43)5-329-337.
Regard,
Muriel. Contribution à l'étude des mouvements d'air dans le bâtiment à l'aide
d'un code de champ. Thèse de doctorat, Lyon: INSA, 2000.
Salliou,
Jean-Rémy. Analyse de l'influence de paramètres géométriques et physiques sur
le coefficient de décharge appliqué à la ventilation dans le bâtiment. Thèse de
Master Recherche, Nantes: Ecole Supérieure d'Architecture de Nantes, 2011.
Swami, M.V., and S. Chandra. "Correlations for pressure distribution on buildings and calculation of natural-ventilation airflow." ASHRAE Transactions, 1988: 243-266.
Follow us on social media accounts to stay up to date with REHVA actualities
0