Performance Risk Assessment– Application Example for Large Atria

Risk assessment has an important issue in design practice for Public Private Partnership projects. However, the use of building simulation tools for risk analysis is not yet common practice. The paper presents a stochastic methodology to efficiently employ building simulation tools in the risk management process. An application example shows its potential.

Keywords: Building simulation, stochastic simulation, uncertainty analysis, risk management, model complexity

A stochastic methodology is presented and applied to efficiently employ building simulation tools in the risk management process. An actual Public Private Partnership (PPP) -project of an atrium in The Netherlands is used for risk treatment decision support. The application showed that a simple assessment approach could already provide guidance either towards potential treatment strategies or more complex assessment approaches. Components of the methodology consist of sensitivity and uncertainty analysis and risk evaluation.

Introduction

Risk can be defined as the product of two contributing factors: the probability of occurrence of a threat and its impact or consequence (de Wilde, 2012) (Munier,2014). Risk assessment of future behaviour of systems enables reduction of unwanted conditions leading, for instance, to less efficient operation of systems or undesired indoor climates.

A new design for a governmental office, in The Hague, has led to the need for assessment of performance risks associated with the indoor climate of the large atria. As the project is developed according to a design, build, finance, maintain and operate (DBFMO) contract, assessment of risks in the design stage of this DBFMO-contract is crucial given the long-term responsibility.  Requirements, and related risks, towards the atrium refer to the installation performance and comfort. Large atria are complex environments. Their (risk) assessment nevertheless can be based on methods ranging from simple (e.g. rule of thumbs and traditional physical calculation methods) up to complex (numerical modelling). However, selecting the right method for the problem is not straightforward (Moosavi et al, 2014) (Morbitzer, 2003).  In some cases, increasing the level of complexity of the model may decrease the accuracy of the results, due to increasing uncertainties in the input data (Kolsaker, 1995).

The main objective of this research therefore was to support the selection of the appropriate building simulation tool for the risk assessment. The atrium case is used as a means to develop the method.

Methodology

Figure 1 presents the developed performance risk management framework. It originates from the framework as proposed by ISO 31000 (2009a, 2009b). Risk identification is the starting point for the analysis. It requires the definition of the Key Performance Indicator (KPI) that reflects the risk, and the variables and its input parameters that affect the KPI. The risk encompasses two factors: Consequence and Probability. Consequences often can be defined in terms of (extra) costs or penalties. In PPP-projects penalties (money) generally will be the consequence of not fulfilling the requirements agreed on. The probability of a risk generally is harder to quantify, as deterministic models often are not applicable, exact values for the input parameters in time and space are usually unknown. To quantify this uncertainty, and with that the probability (e.g., % chance), reference has to be made to stochastic models.

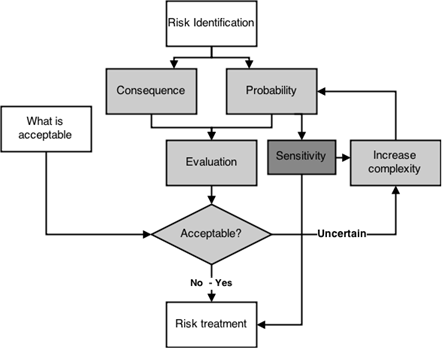
Figure 1. Performance risk management framework.

The stochastic method selected for the uncertainty analysis is the Monte Carlo method. This method gives the probability distribution of possible results by running a simulation model for a number of scenarios and randomly selecting a different set of values from the uncertainty ranges of the input parameters. The number of scenarios depends on the uncertainty ranges, the model and the amount of parameters. To reduce the required computing time in case of large numbers of scenarios and if large simulation models are required Latin hypercube sampling (LHS) can be applied to arrive at a representative probability distribution with less effort (van Goch, 2011) (Hoes, 2007) (de Wit, 2001). Uncertainty analysis gives insight into the influence of the whole parameter set on the risk probability.

Sensitivity analysis can provide additional knowledge on the most influential input parameters. This knowledge can help in focussing on the treatment to reduce the risk most effectively or identify the need to analyse the effect of an input parameter at a more detailed (simulation) level. In this work Monte-Carlo simulation in combination with linear regression analysis is applied. Standardised regression coefficients (SRC) are obtained to quantify the changes of the input parameters relative to the output (Manache and Melching, 2008) (Houben et al, 2010). The input parameter with the largest SRC has the most influence on the output.

Risk Evaluation assesses the combined consequences and probability. The outcome is compared to what is regarded Acceptable. If the uncertainty in the analysis is too large further analysis is required. Outcomes from the sensitivity analysis then can be used to determine whether the current model applied requires more detailed information or a new assessment should be chosen that allows more variables to be included in the analysis. In both ways complexity of the analysis is increased (Increase complexity; Figure 1).

Figure 2 presents a visualization of a generic example of increasing the complexity of the risk evaluation in the two directions identified.

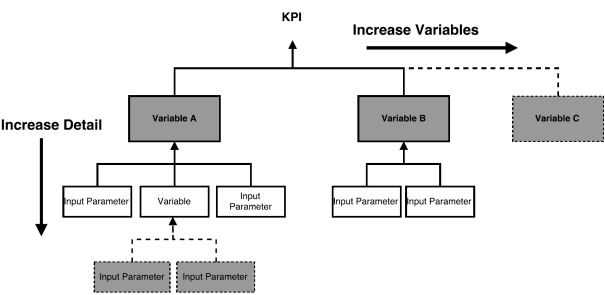
Figure 2. Two ways to increase complexity (generic example).

Application

The presented methodology is applied on the DBFMO-case located in centre of The Hague. The case consists of six atria which have been designed in 1993 as a means to allow office windows to be opened while blocking noise and wind from the immediate surrounding. The atrium is renovated. For part of the atria the indoor thermal requirements decreased (i.e. lower temperatures allowed, till 3°C) while keeping the original atrium façade in place. The office building façade on the other hand was upgraded to have better insulation and air tightness.

For the atrium case, one risk identified was the potential fogging of the atrium windows due to condensation and potential of dripping of water from the ceiling and façade. The risk referred to the visual comfort and the building reputation, with surface temperature and relative humidity level as key variables for assessing the condensation risk. In the original design condensation hours were estimated at approximately 20 hours per year (minimum indoor temperature atrium 12°C; Perquin, and Wapenaar, 1991)

The possible consequences of condensation, comfort and reputation, can be quantified in penalties. Similar penalties are in place for other rooms in the case investigated, e.g., €200 for each hour indoor thermal requirements are not met for more than 12 hours. No values were specified for the investigated condensation risk. Therefore, an assumption was made with an increment in the penalty in case of consecutive condensation hours (5 €/h for 1 hour to 40 €/h for 5 consecutive hours or more).

Figure 3 presents the input parameters and variables that relate to the condensation risk.

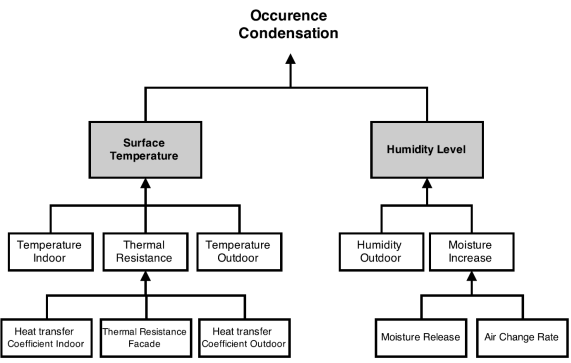
Figure 3. Identification of condensation parameters.

The first approach (model M1) for assessing the probability of the risk would assume the simplest model feasible for the case at hand. In this case a steady-state one-dimensional heat transfer model was chosen where only the atrium façade was modelled. The Monte Carlo method is applied where, apart from the weather data for the location and the façade thermal resistance, ranges for the boundary conditions (Figure 3) were assumed wide and uniformly distributed. Matlab was used for the calculations. Given the simplicity of the model LHS is not required in this case and convergence of the solution was assessed by increasing the number of scenarios to be calculated. Results of the analysis are shown in Figure 4a-c. Figure 4d presents examples of the effect of treating individual input parameters (from regression analysis) on the number of condensation hours.

If the condensation risk is unacceptable more complexity in the model can be introduced, either by increasing the level of detail of the input parameters or by introducing additional variables (Figure 2). For the practical case the moisture release was most sensitive. Moisture contribution to the atrium is obtained from (humid) airflow from the offices into the atrium. This was assessed by assuming an airflow rate with presumed humidity level from the office into the atrium (model M2). Again ranges and a uniform distribution were assumed for these two parameters. As originally a steady-state approach was assumed an additional variable ‘time’ was introduced. For these calculations TRNSYS was used (model T1). Due to computation time now LHS is introduced in the analysis to reduce the number of scenarios required. With 250 scenarios in this case representative results were obtained. In addition, this model was expanded with the extra parameters as identified for model M2 (Model T2). The latter model also included the heat flow into the atrium, which was not considered for model M2.

Figure 5 compares the outcomes (condensation hours) for the four models.

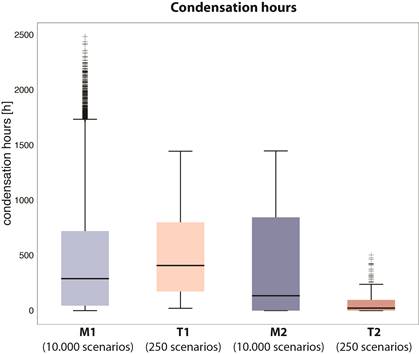
Figure 5. Probability of condensation hours per year for different assessment approaches. (Med= Median, σ= standard deviation) M1 (Med=290, σ= 516), T1 (Med= 409, σ= 386), M2 (Med= 135, σ= 436), T2 (Med=23, σ= 110).

The effect of (thermal) buffering in the transient case is visible in the boxplot outcomes for model T1 compared to the M1 model. The M2 model indicates a reduced but skewed distribution as maximum moisture release is now determined by two input parameters. Finally, the T2 model shows the important aspect of taking the heat transfer from the offices into the model complexity as well. The T2 model simulates an average atrium temperature of 13.2°C compared to 11.9°C for the T1 model. The Matlab models only focus on moisture transfer.

Discussion and conclusion

The application presents an example of the functioning of the model developed. Risk assessment and decision support for treatment selection are useful outcomes in the design process. The application example however did show the importance of providing correct assumptions on the ranges that may be assumed for the input parameters under investigation. Though not easy, this is a critical aspect of the methodology. Nevertheless, the stochastic method and combined sensitivity analysis provide means to visualize this effect and act on it to reduce the risk. In a deterministic method this may be much more difficult to capture. Uncertainty of the result can be reduced effectively by focussing on influential parameters during the selection of the more complex assessment approach.

References

ISO. (2009a). ISO 31000:2009, Risk management – Principles and guidelines (Vol. 2009). International Organization for Standardization.

ISO. (2009b). ISO Guide 73:2009, Risk management – Vocabulary. International Organization for Standardization.

Goch van, T. a. J. (2011). The computational optimization of heat exchange efficiency in stack chimneys. Master thesis, Eindhoven University of Technology.

Hoes, P., Hensen, J. L. M., Loomans, M. G. L. C., Vries, B. d., & Bourgeois, D. J. 2009. User behavior in whole building simulation, Energy and Buildings, vol. 41, no. 3, pp. 295-302.

Houben, J. V. F., Hensen, J. L. M., Trcka, M., & Zanden, W. (2010) Computational Innovation Steering: Simulation-assisted performance improvement of innovative buildings and systems, Proceedings of the System Simulation in Buildings Conference SSB, 13-15 December, Liege, Belgium, p. 20.

Kolsaker, K., & Frydenlund, F. (1995). Simplified models for air stratification and thermal comfort in atria. ASHRAE Transactions, 101(2), 11.

Manache, G., & Melching, C. S. (2008). Identification of reliable regression- and correlation-based sensitivity measures for importance ranking of water-quality model parameters. Environmental Modelling and Software, 23, 549–562.

Moosavi, L., Mahyuddin, N., Ab Ghafar, N., & Azzam Ismail, M. (2014). Thermal performance of atria: An overview of natural ventilation effective designs. Renewable and Sustainable Energy Reviews, 34, 654–670.

Morbitzer, C. A. (2003). Towards the Integration of Simulation into the Building Design Process. PhD Thesis, University of Strathclyde, Glasgow, Scotland, UK.

Munier, N. (2014). Risk Management for Engineering Projects - Procedures, Methods and Tools. Springer International Publishing, Switzerland.

Perquin, G., & Wapenaar, P. (1991). Bouwfysische aspecten van de serres van het VROM-gebouw in Den Haag. Bouwen Met Staal, (99), 25–27.

Wilde de, P., & Tian, W. (2012). Management of thermal performance risks in buildings subject to climate change. Building and Environment, 55, 167–177.

Wit de, M. S. (2001). Uncertainty in Predictions of Thermal Comfort in Buildings. PhD thesis, Delft University of Technology, Delft, The Netherlands.