Predicting personal thermal preferences based on data-driven methods

Abstract

Personal Comfort Models (PCM) is a data-driven approach to model thermal comfort at an individual level. It takes advantage of concepts such as machine learning and Internet of Things (IoT), combining feedback from occupants and local thermal environment measurements. The framework presented in this paper evaluates the performance of PCM and PMV regarding the prediction of personal thermal preferences. Air temperature and relative humidity measurements were combined with thermal preference votes obtained from a field study. This data was used to train three machine learning methods focused on PCM: Artificial Neural Network (ANN), Naive-Bayes (NB) and Fuzzy Logic (FL); comparing them with a PMV-based algorithm. The results showed that all methods had a better overall performance than guessing randomly the thermal preferences votes. In addition, there was not a difference between the performance of the PCM and PMV-based algorithms. Finally, the PMV-based method predicted well thermal preferences of individuals, having a 70% probability of predicting them correctly.

1 Introduction

The prevalent approach for design of thermal comfort in HVAC systems worldwide is based on the Predicted Mean Vote (PMV) model [1, 2]. This model predicts the overall thermal sensation of occupants, based on two personal parameters: metabolic rate, clothing level; and four environmental variables: relative humidity, mean radiant temperature, air temperature and air velocity. However, the method requires data that is difficult to estimate in real applications, such as: metabolic activity rate and clothing level. In addition, the PMV is not able to re-learn from new data since the input parameters it uses are fixed in the model. Lastly, the model had a poor predictability performance when applied to individuals in some field studies [3-5]. In the last years, a new approach to model thermal comfort has been suggested, taking advantage of modern data modelling techniques, named Personal Comfort Models (PCM). They take individuals as units of analysis, where measured data is combined with feedback from occupants to create models that predict individual responses [6]. PCM are based on data that is easy-to-obtain and cost-effective, using machine learning algorithms for data processing. Different algorithms and sources of information can be used, adding flexibility to the data modelling.

The framework described in this report evaluates the performance of three different machine learning techniques and compares them with an algorithm grounded on the PMV model. Data obtained from a participatory sensing assessment in two university offices was used to compare all the methods in terms of the prediction of thermal preference votes. This project contributes with the following: (1) A field evaluation of a thermal comfort web-based survey, (2) A performance evaluation of four methods: Artificial Neural Networks (ANN), Naive-Bayes (NB), Fuzzy Logic (FL) and Predicted Mean Vote (PMV) with regards to thermal preference predictability.

2 Related work

Different approaches to model thermal comfort at a personal level have been made in recent years. Many of the initial attempts originated from multidisciplinary efforts rather than thermal comfort research alone. A number of those studies used the PMV index as the metric to integrate thermal comfort in learning algorithms [7–10]. All of them employed a multi-valued logic called fuzzy logic to characterize different thermal comfort categories given by the PMV. This approach has the limitations of the PMV model: the difficulty to account for personal parameters and is not focused on individuals. As a result, there is a growing interest to develop methods that employ data easy and cheap to measure, taking advantage of state-of-the-art mathematical modelling methods. Different machine learning techniques have been tried depending on the available data and the focus of the method. Bayesian networks was the tool implemented by [11] to model thermal comfort preferences. This framework achieved a 70% accuracy when predicting thermal preference votes from occupants in a field study. The same learning technique was used by [3] to determine comfort temperatures with the ASHRAE RP-884 data base, a set of data used to develop the Adaptive Thermal Comfort Model [12]. The approach showed an improved performance compared to conventional thermal comfort models such as PMV and the Adaptive model. Artificial Neural Networks were implemented by [13] to model thermal sensation. This approach showed 80% accuracy when predicting occupants’ votes in a field evaluation.

Despite the above, there has not been many applications of PCM in field studies for long periods. Fuzzy logic controllers were employed by [14, 15] to model thermal preferences from occupants in offices. That information was used together with ventilation airflow measurements to control a HVAC system for a period of 13 and 14 weeks. The results showed 12–39% airflow reduction and an improvement of thermal comfort when using the methods based on fuzzy logic. However, the performance of a participatory sensing methodology relies substantially on the degree of participation of the occupants. Keeping the consistency of occupants' participation is a challenging task. Different types of survey interfaces were tested by [16], proposing a plain slider scale that improves participation and consistency when carrying out a participatory sensing approach.

To avoid relying on occupants' feedback, several investigations were made to find correlations between human behaviour and thermal comfort. A Personal Comfort System (PCS) was applied by [6], consisting of a device that allowed occupants to regulate the temperature in their local working area, using a custom-built seat. Occupants' behaviour when regulating their local thermal environment was combined with surveyed information and thermal environment measurements. This information was used as input to six different PCM-based machine learning algorithms to predict thermal preference votes. The results showed that the PCM had an average prediction accuracy of 73%, which was better than the performance of conventional thermal comfort models, which only had a 53% accuracy.

The implementation of PCM in real HVAC applications is still a developing task. More field studies are needed to test the performance of data-driven methods when predicting personal thermal responses.

3 Methodology

A field assessment based on a field study was carried out in two offices at the Technical University of Denmark. Thermal preference votes from six participants were obtained continuously during a period of thirteen days. Occupants were provided with a web-based survey that could be accessed either by smart-phones or personal computers. During that period, the thermal environment in the room was modified in a non-systematic manner by opening windows, turning on/off electric heaters and controlling water flows inside radiators. Air temperature Ta and relative humidity RH were recorded periodically every 5 minutes at the local workplace of each occupant by using HOBO-loggers as measuring instruments [17]. This procedure was used to obtain a wide range of thermal preference votes as a result of having different levels of thermal environment inside the offices.

The aim of the evaluation was to characterize the performance of four algorithms when predicting thermal preference categories or classes, generated from the participatory sensing votes. The numerical value of a vote is called Thermal Preference Value (TPV), which can take values between 0 and 18. Three different classes were generated from the TPV as follows: from 0 to 7 corresponded to "Colder", from 8 to 10 were considered as "No change" and 11 to 18 were considered as "Warmer". A thermal preference category with its corresponding Ta and RH measurement formed a data point. The total number of data points gathered along the evaluation period was divided into data used for training and testing the learning algorithms. How good the performance of an algorithm was depended on how well it predicted thermal preference classes based on unseen Ta and RH measurements or testing data. The ratio between training and testing data was optimized in a sensitivity analysis, evaluating the outcome in terms of classification performance. An algorithm that has a good performance of predicting thermal preferences is able to provide an accurate description of occupants' individual comfort zones. Thus, HVAC control systems can benefit from the inclusion of such algorithms to provide an adequate indoor environment, specific for different requirements and working conditions.

3.1. Field study

Occupants were asked to answer a simple question: How would you prefer the temperature? The answer was given in a snapping scale, where it was possible to select: much colder, no change, much warmer or any value in between, as shown in Figure 1 (left). After each vote was made, a graphical feedback was given to every participant, illustrated in Figure 1 (right). This plot showed the total number of daily votes per category in the room to encourage occupants' continued participation. All six participants were requested to vote as many times as they could. They were provided with daily reminders during the evaluation period. The only restriction for the participants was not to vote with a minimum timespan of 15 minutes between votes. This condition was to avoid having persistent occupants expecting to get a rapid change of their current thermal environment. However, all votes were taken into account in the assessment, no matter the period of time between them. The design of the participatory sensing survey aimed to maintain participation along the evaluation period and improve consistency, according to the findings of [16].

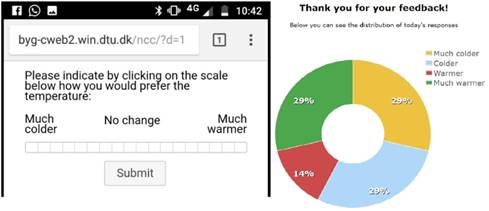
Figure 1. Survey implemented in the field experiment.

3.2. Algorithms

The methods applied in this study provided a rather intuitive application and did not consider a large number of assumptions with respect to the data used to train them. This allowed implementing the algorithms without adjusting many parameters, thus, it was straightforward to determine their optimal performance. A brief description of the methods and considerations taken into account are presented as follows:

3.2.1 Artificial Neural Networks (ANN)

ANN is a method used to solve non-linear problems by using a network composed of individual elements or so-called neurons. In each neuron, different types of mathematical transformations or transfer functions are used. The outcome of this technique is a network where the weight of each neuron has been optimized to minimize the error between the output of the network and the data used for training. ANN was implemented by using the Matlab Artificial Network Toolbox. Three different types of transfer functions were tested: Log-Sigmoid (logsig), Hyperbolic-Tangent Sigmoid (tansig) and Linear transformation (purelin). An iterative process was carried out through a method called Levenberg-Marquardt backpropagation (LM-BP) [18].

3.2.2 Naive-Bayes (NB)

The NB method uses the basic principles of probability, based on the application of the Bayes theorem. This states that the probability of a given event is calculated from previous knowledge about conditions related to an event. In particular, the term "naive" comes from the assumption that different factors that affect the event are independent of each other, also named conditional independence. In this method, it is also assumed that all thermal preference categories or classes have the same distribution. To implement this method, first a Probability Density Function (PDF) was selected and applied to the training data, calculating the mean and standard deviation of each parameter. These two statistical parameters were used to calculate the probability of a certain class of unseen data, used for testing [18].

3.2.3 Fuzzy logic (FL)

FL is a multi-valued logic grounded on the statement that the truth of an affirmation is a matter of degree, first introduced by [19]. Unlike in classical logic where a variable can be either 1 or 0, in FL a variable can also be any value in between those numbers. The data in FL is classified as fuzzy sets, which represent linguistic variables (e.g., hot, cold, low or high). How much a data point belongs to a fuzzy set is given by a membership degree. The framework applied to develop the FL algorithm was based on the study from Jazizadeh et al [14]. This approach was grounded on the Wang-Mendel method to create fuzzy logic descriptive models [20].

3.2.4 Predicted Mean Vote (PMV)

The PMV-based method considered that a PMV index below -0.5 corresponds to a preference towards "Warmer", above 0.5 is associated with a preference to the class "Colder" and values between -0.5 and 0.5 indicate a preference of "No change". The implementation of the PMV model was performed by applying in Matlab the algorithm defined in ASHRAE 55 [21]. Three input parameters to determine the PMV index were varied in the method to establish the best performing configuration in terms of classification performance. The clothing level was varied between 0.5-1.2 [clo] accounting for typical garments for summer and winter respectively; the metabolic activity rate between 1-2.1 [met] was tested, corresponding to a range of physical activities that can be performed in offices, from being seated, relaxed to walking; and the mean air velocity was varied between 0-0.12 [m/s] representing the maximum range allowed in landscaped offices, according to ISO 7730 [22].

3.3 Performance evaluation

Identification of the category or class a new data point belongs corresponds to a classification problem. The algorithms tested in this assessment were evaluated by their capacity to classify thermal preference categories based on thermal environment measurements. How good a classification algorithm (or classifier) performed depended on the number of correct and incorrect guesses. When a data point was correctly allocated in a certain category "A", it was called true positive. Similarly, the data that was correctly not allocated in that category was called true negative. On the other hand, the data that was incorrectly classified as "A" was called false positive. Finally, false negatives were data that was supposed to be "A" but was classified in another category. The True Positive Rate (TPR), also named hit rate or recall, is defined as the ratio between the number of true positives and the total number of positives. The False Positive Rate (FPR) or false alarm rate, corresponds to the ratio between the number of false positives and the total number of negatives. TPR states the proportion of positives correctly classified, whereas the FPR gives the probability of wrongly allocating a category as negative. From TPR and FPR, the Receiver Operating Characteristics (ROC) was obtained [23]. The ROC is a two-dimensional plot, where FPR is placed on the x-axis and the TPR on the y-axis, as shown in Figure 2. This graph represents the trade-off between benefits (true positives) and costs (false positives).

Figure 2. ROC curve example.

The analysis of the classification performance in the framework presented in this report is based on the Area Under the Curve (AUC), which is a scalar number that simply represents the area under the ROC curve. The AUC is equivalent to the probability that a classifier will rank a randomly selected positive event higher than a negative selected one, i.e., the probability that a class will be correctly classified as such [23]. It can take values between 0 and 1, corresponding to the minimum and maximum a classifier can perform. An AUC=0.5 means that the classifier predicts as many positive instances as negative ones, which is called random guessing. Accordingly, values above 0.5 are generated by well performing classifiers and below 0.5 for poorly performing ones. As the aim of the algorithms evaluated in this report was to guess three different thermal preference categories, a multi-class AUC was taken into account. This approach calculates the average AUC of all classes, considering a method called "each class against the rest", represented in Eq. 1 [24]. This method assumes that all classes have uniform distribution, calculating the probability of classifying correctly a class against the others, which is then averaged with the probability from the rest of the classes.

Where AUCmc is the multi-class area under the curve, c is the total number of classes, j is a class and restj represents all the classes different from class j.

4 Results and discussion

During the survey period, occupants were not forced to participate nor to provide a specific number of votes to avoid influencing their everyday activities. Thereupon, the number of votes per participant along the surveyed period varied considerably (Figure 3). In spite of the daily reminders and the simplicity of the survey, a decreasing trend in the number of daily votes provided was observed.

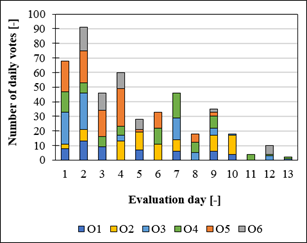
Figure 3. Number of daily thermal preference votes provided by each occupant along the evaluation period.

Table 1 illustrates the statistical characteristics of the TPV resulting from the assessment. The table shows a lack of variability in the votes, considering that occupants could vote within the TPV range between 0 and 18. A narrower range of TPV was obtained because of the reduced variation in the air temperatures (Table 1). The percentiles show that the votes were mainly biased towards low TPV associated to the category "Colder". This result suggests that the occupants were in general more affected by warmer temperatures in the room than the opposite. Thus, the data provided to the algorithms was not equally distributed among the three classes considered, a problem called imbalanced data. In addition, the percentiles reflect that the classes were not uniformly distributed, i.e., the probability of predicting a vote within a class was not constant. As described by [24], uniform distribution is a basic assumption to evaluate the classification performance of an algorithm by using the multi-class AUC described in Eq.1. In practice, it is difficult to have approximately the same number of TPV values in each class per occupant. Occupants would need to be exposed to different thermal environment conditions during equal periods of time when obtaining the training data. It is therefore a challenging task to characterize accurately the classification performance of a learning algorithm that aims to predict occupants' thermal preferences.

Table 1. Statistical parameters of the TPV per occupant obtained from the evaluation. O: Occupant, STD: Standard deviation.

The percentiles and standard deviations in Table 1 show that occupants 1, 5 and 6 provided votes with higher variability. The feedback from those three occupants were chosen as input data to test the learning algorithms and compare them with the PMV method. The reason was to ensure that all the thermal preference categories had sufficient data points, minimizing the effects of imbalanced data.

Figure 4 shows that all methods had a better performance than random guessing (AUC=0.5) thermal preference categories. Therefore, all classifiers will probably predict more positive instances than negative ones. This shows a good performance considering that only Ta and RH measurements were provided to the methods. The classification performance among the occupants was mainly affected by how many votes per occupant were provided, the distribution of the data points among the classes and the consistency of the votes from the occupants. Higher AUC values could be achieved if any of those factors were improved. The inclusion of data from additional parameters, such as radiant temperature and air velocity, could also improve the classification performance of the algorithms tested.

Overall, the methods with the highest performance were NB and PMV, accounting for a probability of correctly predict a class of 73% and 70%, respectively. The NB method assumed that Ta and RH were independent from each other. It calculated the mean and standard deviation of the training data, adjusting a PDF. Hence, it did not calculate individual factors related to each data point. That was the reason why it performed better than the other algorithms. By calculating variables that comprise a whole data set, it simplifies the learning process.

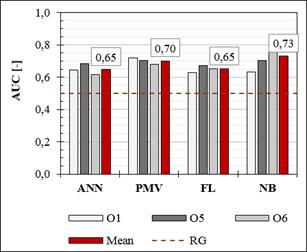
Figure 4. Classification performance represented by the AUC value for all four algorithms studied, taking into account the data obtained from occupants 1 (O1), 5(O5) and 6(O6). RG=Random Guessing line.

Figure 5 shows the performance of all methods with regards to each thermal preference category. Classifying incorrectly a category could yield to serious operational problems when applied in reality. Thermal comfort and health could be compromised when a HVAC control system regulates the thermal environment wrongly. For instance, controlling an indoor environment based on a preference towards colder temperatures instead of warmer, could have serious implications in occupants' well being. Figure 5 shows that all methods except FL had a better performance when predicting the "No change" category than any other class. This is owed to the unbalanced data among the classes, presented in Table 1.

Some machine learning methods were more sensitive to imbalanced data than others were. They tended to favour the "no change" class for having the largest proportion of data, translated in a larger amount of true positives. In that context, the NB method exhibited less difference in the prediction of different classes. This method reduced the influence of biased data by assuming that all classes had the same PDF and by calculating parameters that enclose a whole data set. To avoid the problem of imbalanced data, it would be needed to expose people under uncomfortably warm/cold environments for a period equal to the period they feel comfortable. Since the last is unlikely to be applicable in reality, it is desired that the algorithm employed to predict thermal preferences overcomes the problem of not uniformly distributed classes. For that, it is proposed to make a sensitivity analysis of a classifier changing the distribution of the training data per class [25].

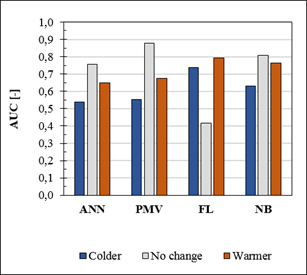
Figure 5. Classification performance represented by the AUC value for all four classifier studied, taking into account the three thermal preference classes predicted.

A correlation between the amount of training data needed by the learning algorithms and their corresponding classification performance is illustrated in Figure 6. This information allows the identification of how much the number of votes can be decreased with regards to the variation of the performance of a method. The data of all the occupants was combined and a linear correlation was applied for comparison purposes, even though the actual correlation may not be linear. A single data point corresponded to a thermal preference category with its corresponding measurement of Ta and RH (only Ta for the FL method). Figure 6 illustrates that all the methods had a performance better than random guessing, even when the amount of training data was reduced to only 10 data points. The NB was not only the best performing method, but also required less data to generate a higher AUC compared to the other algorithms. The performance of NB and ANN increased with an increase of the amount of training data, whereas the FL method diminished its performance. Unlike the two other learning methods, FL does not rely on an iterative process to diminish the error during the training process of the algorithm.

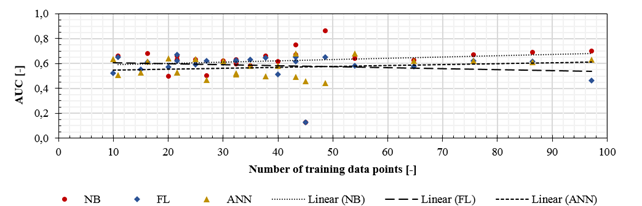
Figure 6. Classification performance represented by the AUC value as a function of the amount of data required for training on each of the three learning algorithms analysed.

When training the FL method, the first part of the training data read by the algorithm was used to construct the fuzzy sets. The rest of the training data did not contribute to create better fuzzy sets, as they were already created by the first data points read. Thus, providing more data point to the FL algorithm did not improve its performance.

5 Limitations

There are a number of limitations with regards to the framework proposed in this assessment. First, the evaluation period considered in the field assessment was limited. A longer period would allow having more input data for the learning algorithms, accounting for variations that the thermal preferences may have with different weather conditions. As a result, the classification performance of the PCM-based algorithms could be analyzed with more training data. Second, miss-classification costs, i.e., the cost of not classifying correctly a category, were not taken into account. In reality, it does not have the same implications to classify a "Warmer" category as "No change" than classifying it as "Colder". This should be taken into account when characterizing the performance of PCM, especially when implemented in real applications. Third, it was considered that TPV was mainly influenced by air temperature and relative humidity. It would be needed to determine the required number of votes per occupant to minimize the influence of other factors that may influence the thermal preference votes. This will help to define the minimum number of votes per occupant needed to ensure a desired classification performance.

6 Conclusions

Personal Comfort Models (PCM) allow to focus on the thermal comfort needs of individuals based on local indoor environment measurements and feedback provided by them. Three PCM method and a PMV-based method were tested in this assessment. From the results obtained in this assessment, the conclusions were the following:

·         When predicting personal thermal preferences, all the four algorithms tested (ANN, NB, FL and PMV) showed a better overall performance than guessing randomly, even though only air temperature and relative humidity were provided as input data.

·         The difference between the performance of the PCM-based methods and the PMV-based method was very modest.

·         The PMV method was capable of predicting thermal comfort at an individual level, with a probability of guessing correctly 70% of personal thermal preference votes.

·         The NB method was not only the best performing method, predicting 73% of the thermal preferences, but also performed better at predicting each thermal preference category, requiring less training data than the other methods.

Future research efforts will be focused on the implementation of PCM in HVAC control loops, focusing on easy-to-obtain data. A field study for a long period will be considered in future assessments, accounting for the challenge of maintaining occupants’ participation.

References

1.  P.O. Fanger, Mc. Graw Hill (1970).

2.  B. Olesen, KC. Parsons, Energy Build., El Sevier,34, 537 (2002).

3.  F. Auffenberg, 2547 (2015).

4.  J. Kim, Build. Environ., El Sevier, 132, 114 (2018).

5.  J. Van Hoof, Wiley Online Library, 18, 182 (2008).

6.  J. Kim, Y. Zhou, S. Schaivon, Build. Environ., El Sevier, 129, 96 (2018).

7.  P. Bermejo, L. Redondo, L. de la Ossa, Energy Build., El Sevier, 49, 367 (2012).

8.  D. Kolokotsa, G. Saridakis, A. Pouliezos, G. Stavrakakis, Energy Build., El Sevier, 38, 1084 (2006).

9.  F. Calvino, M. La Gennusa, G. Rizzo, G. Scaccianoce, Energy Build., El Sevier, 36, 97 (2004).

10.L. Hang, D. Kim, App. Sci., 8, 1031 (2018).

11.A. Ghahramani, F. Jazizadeh, B. Becerik-Gerber, Energy Build., El Sevier, 92, 86 (2014).

12.R. De Dear, G.S. Brager, Transactions, ASHRAE, 104, 145 (1998).

13.W. Liu, Z. Lian, B. Zhao, Energy Build., El Sevier, 39, 1115 (2007).

14.F. Jazizadeh, A. Ghahramani, B. Becerik-Gerber, Energy Build., El Sevier, 70, 398 (2014).

15.A. Ghahramani, F. Jazizadeh, B. Becerik-Gerber, Energy Build., El Sevier, 85, 536 (2014).

16.F. Jazizadeh, F. Marin, B. Becerik-Gerber, Energy Build., El Sevier, 68, 140 (2013).

17.C. C. Onset, https://www.onsetcomp.com (2018).

18.M. Mørup, M.N. Schmidt, M. Mørup, Technical University of Denmark (2018).

19.L. Zadeh, Trans. on fuzzy syst., IEEE, 4, 103 (1996).

20.L. Wang, J. Mendel, Trans. On syst., man and cyb., IEEE, 22, 1414 (1992).

21.A.S.H.R.A.E., Standard 55-2013 (2013).

22.E. ISO, Standard 7730:2005 (2005).

23.T. Fawcett, Pat. Rec. Let., El Sevier, 27, 861 (2006).

24.C. Ferri, J. Hernandez-Orallo, R. Modroiu, Pat. Rec. Let., El Sevier, 30, 27 (2006).

25.H. He, E. Garcia, Tran. On Know. Dat. Eng., IEEE, 21, 1263 (2009).