Air Conditioning of St Mary’s Archeological Church, Cairo

Essam E. Khalil

Prof.Dr

Faculty of Engineering, Cairo University

Cairo –EGYPT

Airflow characteristics in ventilated and air-conditioned spaces play an important role to attain comfort and hygiene conditions. This paper utilizes a 3D Computational Fluid Dynamics (CFD) model to assess the airflow characteristics in ventilated and air-conditioned archaeological Church of Christ (hanging Church) in Cairo, Egypt. It is found that the optimum airside design system can be attained, if the airflow is directed to pass all the enclosure areas before the extraction with careful selection of near wall velocities to avoid any wear or aberration of the wall paintings. Still all commonly known factors and evaluation indices have the shortage to describe the influence of the recirculation zones on the occupancy zone of the visitors and also on the fresh supplied air. The mode of evaluation should assess the airflow characteristics in any passage according to its position in the enclosure and the thermal pattern and air quality. The paper ends with brief discussion and concluding remarks.

Introduction

The present work raises several questions in the room airflow motion prediction techniques. This article presents the results of an ongoing evaluation of a CFD based on computer models for predicting room airflow distribution in the Hanging Church in Egypt. To design an optimal HVAC airside system that provides comfort and air quality in the conditioned spaces with good energy efficiency is a great challenge. For this project a numerical study is carried out to define the optimum airside design of the HVAC systems, providing optimal comfort and healthy conditions energy efficiency. A CFD program is used. Basically, various airside designs are considered including floor and or ceiling supply, different obstacle and alternative positioning to introduce the capability of each design to provide the optimum air flow characteristics. The optimum utilization of the air movement to condition and ventilate can be attained by properly locating the supply diffusers and extract grills to minimize the recirculation zone and prevent the air short circuits. Ideally, the optimum airside design system can be attained, if the airflow is directed to pass all the enclosure areas before the extraction,Berglund, L. G., and Cain, W. S. (1989). The primary objective of the project is to demonstrate the capabilities of the numerical tool to predict the airflow characteristics and thermal patterns in the different conditioned church configurations in view of basic known flow characteristics, Khalil (2008 and 2013). The numerical model is used to investigate the airflow pattern, temperature and relative humidity distributions inside the church main hall.

Figure 1 shows the church main hall while Figure 2 depicts the hideaway location where baby Christ used to be hidden during the journey of the sacred family from Palestine to Upper Egypt. The church that was built over 1 500 ago suffered from adverse effects of excessive humidity and it was proposed to air condition this archaeological monument among the restoration plans that also included the nearby Coptic Museum.

Figure 1. Church Main Hall.

Figure 2. Sleeping hideaway place of Baby Christ in basement.

The design of such facility didn’t allow any alteration in the structure nor the bearing walls of the church that comprised a main hall and neighbouring rooms and facilities. There are students’ chapel, First Floor Chapel as well as the main Nave. The main hall is of 17.2 m x 18.2 m length and width with a height which is variable with domes maximum of 9.3 m, and a total volume of 2 424 m³. Full load estimation was carried out to obtain the maximum cooling capacity requirement at the worst prevailing climatic conditions in Cairo summer. Hourly air system simulation results were obtained for the months of June, July and August. The cooling capacity for the main Nave was 280 kW while for the other chapels these were of the order of 40 kW for the students’ chapel, 40 kW for the ground floor and 36 kW for the first floor Chapel. The cooling plant was designed on the bases of five units each 90 kW to cover the whole complex.

Figure 3 depicts the roof top cooling units used for the main church and the adjoining chapels. The VRV units were used for the Coptic museum.

Computational technique

The present CFD computational procedure includes the numerical solution of the governing equations of mass, momentum, species concentration and energy in three dimensional configurations based on Launder (1972) and Spalding and Patankar (1974). A two equation k-ε turbulence model was used to represent the turbulence characteristics of the flow through the numerical solution of an equation of the kinetic energy of turbulence k and its dissipation rate ε. More than 1,000,000 tetrahedral control volumes were used and numerical convergence was better that 0.001%. Further details of the SIMPLEC numerical algorithm imbedded in FLUENT can be read in detail in references by Khalil (2013).

Model Architecture (Structure)

The church is located in Cairo; the main hall is modelled as shown here in Figure 4a & b.

Figure 4a. Isometric View for the Church Main Hall.

Figure 4b. Arrows indicate location of air inlets through naturally openings in the roof.

Inlet air conditions

The inlet air conditions are based on the average day max of 40ºC and 30% relative humidity, Egyptian Code, representing August climatic conditions. The main hall is of 17.2 m x 18.2 m x height which is variable with domes maximum of 9.3 m, with total volume of 2 424 m³.

Air inlets

The air inlets are set as velocity inlet boundary conditions where velocity was set to be 1.5625 m/s with a total of 12 air inlets, each of 0.4 m² of area (shown by arrows in Figure 4b). This resulted in a total flow of 7 m³/s. The inlet air temperature was set to 287 K, with an absolute humidity of 8 gr/kg. The ACH is chosen to be about 10.

Outlets

The air outlets are set as outflow conditions.

Walls

The walls are considered as a slab to have zero heat flux. The no slip condition is enabled for all walls, while using the standard wall function for near wall treatment.

Visitors Representation

The visitors’ bodies are considered as isothermal walls with a temperature of 310 K. The visitors’ faces are considered as isothermal walls kept at the human skin temperature of 310 K as well. Also it is assumed that there is a specified species mass fraction of 0.0411 kg_w/kg_d.a in order to take into account the sweat effect in moisture gain, Olesen (2000). For carbon dioxide, a diffusive mass fraction of 0.0474 kg_co2/kg_d.a is chosen.

Air circulation

The church hall model design included 12 air supply diffusers, each situated in between the ceiling arcs. The return grills were situated near the ground.

Number of Visitors

The model was used to simulate the situation during a prayer; consequently, the total number of visitors was set to 150 people. The total thermal load was 280 kW cooling, fresh air 1 350 l/s. Loads from solar gain were 3 kW, roof thermal transmitted loads were 69 kW while ventilation load was 79 kW.

Results and discussions

Velocity Predictions

Velocity contours indicated the penetration of the ceiling supply jet till almost above the occupancy zone. The jet flow towards the extract grilles locations as shown at Z=0 and Z=18 m. Figure 5 shows the corresponding velocity contours at X=15 m which is near the other end of the church width as X varies between 0 and 17.2 m. Figure 6 shows the velocity contours in a transverse section at Z=12.15 m and indicated the prayers standing locations. The velocities at these locations are well below 0.25 m/s which ensured the disappearance of any drafts for the comfort of prayers and visitors.

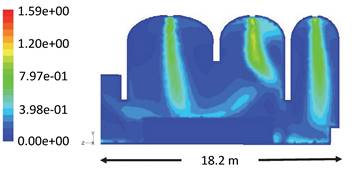
Figure 5. Contours of Mean Velocity In Y Direction, m/s at Y-Z Plane X=15 m.

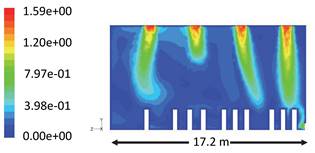
Figure 6. Contours of mean velocity in X-Y plane, m/s at Z=12.15 m.

Thermal Patterns

Energy equation was solved to yield the temperature distribution at the various locations taking into account the heat dissipated from the humans, equipment and also the external heat sources in summer. Figure 7 indicated the temperature contours at a Y-Z plane at X=4 m; temperatures are found to be homogeneously distributed and ensured comfort conditions. Figure 8 represents thermal patters in transverse plane; one can easily see temperatures of 30°C at the seating and standing locations. The remaining zones are at lower temperatures that can be as low as 17°C, bearing in mind that the on coil temperature leaving the ceiling supply grilles are typically 13°C.

Figure 7. Temperature contours, K, in a Y-Z plane at X=4 m.

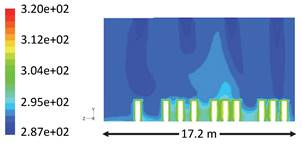
Figure 8. Temperature contours, K, at X-Y plane at Z=12.15 m.

Relative humidity Predictions

The relative humidity contours at various locations in the church are shown here in Figures 9 and 10 at Y-Z at X=4 and 15 m respectively. The local values of Rh% are around 50% at the occupancy level as clearly indicated in the figures above, the cooled supply air leaves the supply grilles at much higher values of 80% and more. Some disperse locations at near 1.8 m above floor indicated high Rh% due to the presence of candles and equipment. Figure 11 indicates some high values of relative humidity at the vicinity of the occupants’ faces.

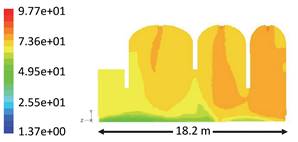
Figure 9. Contours of relative humidity, % at Y-Z plane at X=4 m.

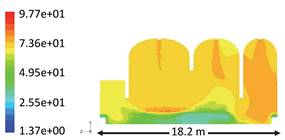
Figure 10. Contours of relative humidity, %, at Y-Z plane at X=15.

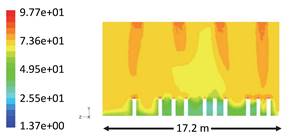
Figure 11. Contours of relative humidity, % at Y-X plane at Z=12.15 m.

Assessment and Validation

Measurements of mean air temperature and relative humidity percentage were obtained with the aid of a hotwire anemometer and electronic hygrometer with accuracy of ±5%. These were compared to the corresponding predictions in Figures 12 and 13. Qualitative agreements were demonstrated, with some discrepancies that are equally attributed to both experimentations accuracies and modelling assumptions.

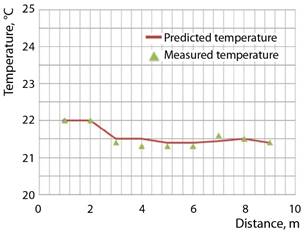
Figure 12. Measured and predicted air temperature at 1.0 m above floor in church.

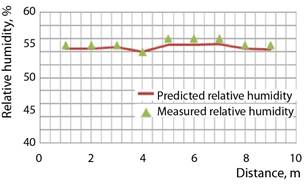
Figure 13. Measured and predicted RH % at 1.0 m above floor in the Church.

Conclusions

From the previous results, one can conclude that the airside designs have a strong influence on the relative humidity distribution and consequently on the IAQ. The location of the supply outlets plays the major role in this distribution. The extract grills should be located in the right location to ensure comfort. Due to the architectural design restrictions of archaeological buildings such as in this church, designers should perform this calculation exercise to properly select the locations of supply and extract grilles in renovated systems in ancient buildings to yield better air flow, temperature, relative humidity behaviour.

References

1.      ASHRAE Handbook, Fundamentals 2013, ASHRAE, Atlanta, USA.

2.      Berglund, L. G., and Cain, W. S., 1989, Perceived air quality and the thermal environment, The Human equations: Health and Comfort, Proceedings of ASHRAE/SOEH Conference IAQ’89 ATLANTA: ASHRAE, pp. 93–99.

3.      Cho, Y., Awbi, H. B., and Karimipanah, T., 2002, “A comparison between four different ventilation systems”, ROOMVENT 2002, 181–184.

4.      FLUENT, 6.2.Fluent Inc., 2009.

5.      Green, G. H., 1982, The positive and negative effects of building humidification, ASHRAE Transactions, 88(1): 1049–1061.

6.      ISO EN 7730, 2005, Moderate thermal environments – Determination of the PMV and PPD indices and specification of the conditions for thermal comfort, International Standards Organization, Geneva.

7.      Khalil, E. E., 1999, Fluid Flow Regimes Interactions in Air Conditioned Spaces, Proc. 3 rd Jordanian Mech. Engineering Conference, pp. 79, Amman, May 1999.

8.      Khalil, E.E., 2008, On the Modelling Of Thermal Comfort and Air Quality in Air Conditioned Healthcare Applications”, International Review of Mechanical Engineering, IREME, March Issue, Vol 1 N° 2, 2008

9.      Khalil, E.E., 2013, Air Distribution in Buildings, Taylor and Francis, CRC Press, USA, 2013

10.    Launder, B.E., and Spalding, D.B. 1974, The numerical computation of turbulent flows, Computer Methods App. Mech., pp. 269–275.

11.    Olesen, B. W., 2000, Guidelines for comfort, ASHRAE Journal, page 41–46, August 1998.

12.    Spalding, D.B., and Patankar, S.V. 1974. A calculation procedure for heat, mass and momentum transfer in three dimensional parabolic flows, Int. J. Heat & Mass Transfer, 15, pp. 1787.