Comparative performance analysis of floor heating systems

From a practical point of view the intermittent operation of underfloor heating systems is challenging due to the heating-up times resulting from the heat capacity in the floor. That is why several floor heating systems have been analysed in a comparative simulation study. It has been observed that heating-up times highly depend on installation heights and structures of the floor heating systems. The study shows in particular that some of the available renovation systems react up to three times faster than standard system.

Introduction

This article deals with the comparison of the heating-up times of four different floor heating systems: a standard wet system and three renovation systems with lower installation height. The renovation systems are the wet system K and two dry systems C and T. The dry-system T is characterized by a special heat conduction plate and the system C by the absence of an insulation layer. By using a transient coupled CFD simulation, the processes of heat conduction, heat radiation as well as the convective heat transport due to the air- and water flows are calculated.

The four systems show a different dynamic of the heating-up times. Table 1 gives an overview about the layers of the four systems.

Table 1. Layer of the floor heating systems from top down.

Methodologies and boundary conditions

Figure 1 shows the layer of the floor heating system by the example of the T dry system. One can see very well, how the heating pipes are surrounded by the heat conduction plates. This heat conduction plates with a thickness of 0.25 mm are modelled fully three dimensional in the simulation model.

The four different systems are simulated in a test cabin made of 200 mm thick aerated concrete walls with a base area of 3 m x 3 m and an interior height of 2.75 m without openings, see Figure 2. Related to the floor area of 9 m² a laying distance between the pipes of 150 mm leads to a pipe length of about 57.7 m and a laying distance of 125 mm results in a pipe length of 69.2 m.

Figure 1. floor heating system T with heat conduction plates; reference: www.bba-online.de.

Figure 2. Geometry of the test cabin and meshing of the wall layers and laying patterns of the floor heating.

Transient, coupled simulations of the test cabin, underfloor heating system, water flow and room air flow are done for all four systems. For the evaluation, the surface temperatures and their local distribution as well as the water temperatures are evaluated in detail as a step response when switching on the underfloor heating system. Furthermore, the enthalpy flows between the water inlet and outlet and the (convective and radiative) heat flows from the floor are evaluated.

The numerical model considers the following aspects:

·         three-dimensional non-isothermal water flow inside the pipes

·         three-dimensional thermal conduction within the inner walls of the pipes as well as within all other layers in the respective floor structure

·         three-dimensional heat conduction within the side walls of aerated concrete

·         non-isothermal turbulent simulation of the air flow in the test cabin taking into account the radiation heat exchange within the test cabin

Results and Conclusion

The initial condition is a uniform temperature of all zones of 15 °C at the start time and a constant fluid in the test cabin as well as in the floor heating tube.

For the water inlet the mass flow rate into the heating pipes is set to 0.025 kg/s with a supply temperature of 35 °C. There is no heat loss assumed below the lower screed layer and on all sides of the floor structure. The calculations are done over a period of six hours of simulated real time. This period is chosen to ensure that in each of the four systems the desired mean surface temperature of the floor area of 24 °C is reached. The calculated flow velocities are less than 0.1 m/s in the tubes.

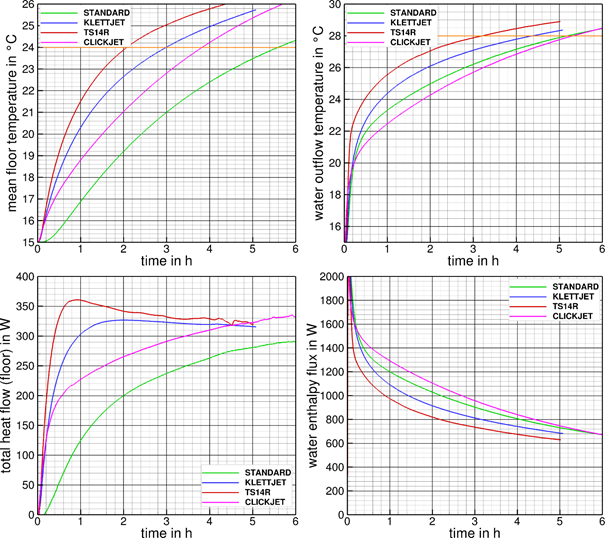
Figure 3. Step responses; from top left to bottom right: time profile of medium surface temperatures of the floor, time profile of mean return temperatures of the water, time profile of total heat flows of the floor, time profile of resulting enthalpy fluxes of the water; in each case for all four systems.

Figure 3, on the left in the upper part, shows the mean surface temperature profiles of the four different systems. The right side represents the corresponding profiles of the water return temperatures. In addition, the total thermal heat flows (convection and radiation) emitted by the respective floor as well as the resulting enthalpy fluxes transferred from the water to the respective floor structure are shown in the diagrams in the lower part of Figure 3.

The different dynamics of all four investigated systems can be clearly seen from the diagrams. Due to the much larger thermal mass of the heating screed, the STANDARD system has the biggest inertia, which results in a slower heating of the tiles and thus also a slower increase in the heat dissipation of the floor heating as a whole. The K system is more dynamic than C due to its insulating layer preventing heat to be transferred into the building structure rather than to the room. Due to the insulating layer, the heat flow into the screed below it is significantly lower than in the C-system. This is also shown by the overall higher enthalpy flux which C-system’s water gives to the surrounding floor layers (see Figure 3, bottom right). In this case, however, a higher heat flow through the tube walls occurs due to the smaller internal diameter of the tube and the associated higher velocity of the water. The good thermal insulation downwards as well as the very good heat distribution upwards over the heat conducting plates lead to a very high dynamic in the system T. The required average floor temperature is reached three times faster than with the system STANDARD. The T-system has been identified as a fast reacting underfloor heating system where the highest overall heat output of the floor is observed with the lowest enthalpy flux of the water during the heating phase. The energy transfer from the water to the chamber is therefore the fastest in this system.

The described facts can also be found in the representation of the temperature distributions of the different configurations, see Figure 4. If more energy has to be distributed in the floor, the system becomes slower.

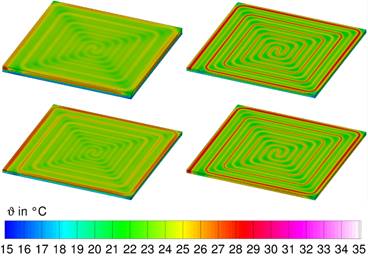
Figure 4. Surface temperatures of the whole underfloor heating system, after reaching a mean surface temperature of 24 °C, view from above; from top left to bottom right: the STANDARD-system and the systems K, T, C.

If a parquet floor is modelled instead of the floor tiles, all systems react much slower due to the lower heat conduction of the wood layer. The differences between the floor heating systems analysed are smaller. However, this wooden surface layer leads to an equalization of the surface temperatures. The ripple of the temperature profiles is significantly lower in all four systems than in the case of the floor construction with tiles.