Estimation of Cross-Ventilation Through Roof Windows in Attics

EN 16798-7:2017 considers that windows on roofs that have a pitch below 60° are not included on the windward side whatever their orientation. It means that roof windows are accounted for, but only on the leeward side when using the existing standard for calculation of air flows, EN 16798-7:2017 [1].

Therefore, in the specific case of a room only equipped with roof windows (e.g. an attic) and aeraulically independent from the rest of the building, whatever the orientation of the roof windows, only the simplified “single-sided” calculation method of EN 16798-7:2017 is applicable.

However, this study has shown that, for a building with low buildings surrounding it, the simplified single-sided method from EN 16798-7:2017 was underestimating the airflow rate by up to 77%.

Keywords: Cross-ventilation, roof window, attic, EN 16798-7:2017, calculation method

According to EN 16798-7:2017, roof windows always have a negative Cp. So, the existing simplified cross-ventilation method from EN 16798-7:2017 cannot be used in the case of this attic. Therefore, when using the existing standard, the simplified single-sided equation shall be used to calculate the airflow rate in this attic, as there are no other options.

The existing simplified single-sided method from EN 16798-7:2017 will be used as reference to be compared with the new developed method.

Theoretically, it is actually possible that an airflow rate due to cross-ventilation occurs through 2 roof windows. According to the literature, a roof window may indeed have a positive wind pressure coefficient when the wind is attacking straight onto the roof, contrary to facade windows for which the coefficient is almost always negative when the wind angle is 45° (see Figure 1).

Figure 1. Wind pressure coefficient data from (Liddament 1996) for a rectangular building for 2 different shielding conditions.

In this study, it is assumed that Cp coefficients are constant for a roof pitch between 30–60 degrees. In the following example, a roof with a pitch of 45 degrees has been considered as illustrated in Figure 2. A linear extrapolation was used on Cp coefficient from Figure 1 (see green markings in Figure 1 for the line “Roof > 30° pitch”) for wind angles between 0° and 45°.

As the Cp depends on the surrounding of the building, if the building is surrounded by obstructions equal to:

·         half the height of the building (left table), then Cp is positive for wind angles between −30° and +30°

·         the height of the building (right table), then Cp is positive for wind angles between −12° and +12°.

Figure 2. Wind directions that induce positive pressure coefficients on roof and facade windows.

Figure 2 compares wind directions that induce positive Cp coefficients for roof windows and facade windows. It highlights that the wind angle that induces positive Cp coefficient is narrower for roof windows than for facade windows. Moreover the range is reduced by roughly 60% if the building is surrounded by buildings with the about same height rather than half the height.

As EN 16798-7:2017 only divides the building into 4 orientations, it considers that Cp coefficients for roof windows are always negative. Therefore, according to EN 16798-7:2017, cross-ventilation cannot occur when there are only roof windows in a ventilation zone (e.g. in an attic).

Objective and method

The objective of this study is to test a new method, based on a EN 16798-7:2017 method (called the “adapted cross-ventilation method”), to take into account cross-ventilation occurring through roof windows and find the impact on estimated ventilation airflow rate. The principle of this new method is, when a zone with only roof windows is simulated, instead of dividing the plan into 4 zones, to divide the plane into:

·         6 orientations (=360°/60°, where 60° is the range for positive Cp values) when the zone is surrounded by obstructions half its height (case 1)

·         15 orientations (=360°/24°, where 24° is the range for positive Cp values) when the zone is surrounded by obstructions of the same height (case 2).

Test Case

Figure 3. Illustration of the test case.

The test case is an attic aeraulically independent from the rest of the building. The roof is a two-sided roof with a pitch of 45° and equipped with one roof window on each side of the room.

The hypotheses used are detailed in Table 1.

Table 1. Hypotheses of the calculation.

The following configurations have been considered for the test case (Table 2):

Table 2. Configurations considered for the test case.

EN 16798-7:2017 method for cross-ventilation

Simplified formulas for cross-ventilation cannot be used in our test cases as there are no facade windows, however, this is the method that has been used to develop the “adapted method”.

To calculate the airflow rate coming in and out of a ventilation zone when cross-ventilation occurs, EN 16798-7:2017 proposes a simplified method based on the following equation:

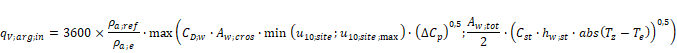
Where the calculation of Aw;cros, representing the equivalent cross ventilation area, is made through an algorithm that divides the building into four orientations and calculate the window opening area in each (see EN 16798-7:2017).

The calculation of the airflow rate due to wind takes into account roof windows only on the leeward side (never on the windward side).

Adapted cross ventilation method for roof windows

To take into account the fact that cross-ventilation may occur through roof-windows located as described in our example, in this study, instead of dividing the plane into 4 angles of 90° each, it will be divided into:

·         Case 1: 6 angles of 60° (Nang = 6)

·         Case 2: 15 angles of 24° (Nang = 15)

Results from this equation will be named “Adapted cross-ventilation method from EN 16798-7:2017” and will be compared to the simplified single-sided method.

More information on the calculation method proposed in EN 16798-7:2017, including the validation of simplified formula with a pressure code, can be found in (Leprince, Valérie; Carrié, François-Rémi, 2016) and (Larsen et al. 2018).

Results

The graphs in Table 3 compare the ventilation airflow rates calculated with the simplified single-sided method from EN 16798-7:2017 (dark green bars) and the ventilation airflow rate calculated with the “adapted” cross-ventilation method (which takes into account cross ventilation that can occurs in a zone or room with two roof windows) illustrated in light green bars.

Results for wind speed from 1 to 5 m/s show an important difference between case 1 and case 2 (see table 3):

·         when the building is surrounded by buildings of its own height (case 2) there are little differences between the simplified single-sided method of EN 16798-7:2017 and the adapted cross-ventilation method. For 25 out of the 42 cases studied, results are the same and the maximum difference is 28% when wind is the main driver (hence small temperature difference and high wind speed)

·         when the building is surrounded by building equivalent to half its height, the difference is significant: only 11 out of the 42 configurations studied provide the same results, the maximum difference reaches 77% and is observed for 11 configurations.

For case 1, with the adapted cross-ventilation method, the wind is the main driver for ventilation from 2 m/s as long as the temperature difference remains below 20°C. This is shown by the airflow rates seen in the light green bars being constant (for a given wind speed above 2 m/s, they are all having the same height whatever the temperature difference).

The results also show that, for a given case, wind speed and temperature difference, differences in percentage between the 2 methods do not depend on the free window area (as in both methods the flowrate is proportional to the free window area).

Table 3. Results for the simulations for case 1 and case 2.

Conclusions

The objectives of this study were:

·         to develop a more precise calculation method adapted to roof windows to take into account cross-ventilation that may occur through them (even when there are no facade windows in the zone)

·         to compare results obtained with this method to the simplified single-sided method from EN 16798-7:2017

The “adapted” calculation method developed is consistent with the one proposed in EN 16798-7:2017, but simply further divides the horizontal plane to better take into account the specific cases of roof windows. The “adapted” method developed shall only be used for the specific case of zones with only roof windows with multiple orientations. As the Cp coefficient remains positive for a wider range of angles for facades windows (see Figure 2), applying this new method to zones with facade windows may lead to falsely consider cross-ventilation. Combining the two methods would lead to much more complex algorithms.

In this study, where roof windows could have positive Cp values even if they have a pitch between 30-60 degrees, we have shown, that:

·         in case 2 (building surrounded by hight obstacles), the new “adapted” cross-ventilation method provides results close to the simplified single-sided method from EN 16798-7:2017,

·         in case 1 (building surrounded with lower building) cross-ventilation can theoretically occur quite often and the simplified single-sided method from EN 16798-7:2017 highly under-estimates the average airflow rate in this specific case.

Proposing this new adapted method for cross-ventilation to calculate the airflow rate in the specific case of room with only roof windows would allow to better estimate the airflow rate in the room. This new “adapted” cross ventilation method could be used as an addendum to EN 16798-7:2017 for the EPB standard systematic review for this specific application of zones with only roof windows.

Nevertheless, while interpreting those results the following limitations shall be kept in mind:

·         The given airflow rates are averaged airflow rates which by no mean are instantaneous airflow rates, assuming (among other things) an equiprobability of wind directions which may not be relevant in certain places

·         Simplified equations used here have been developed in the context of EN 16798-7:2017 and compared to models performed in CONTAM and to on-site measurements (see (Larsen et al. 2018; Leprince, 2016.)). They slightly underestimate the airflow rate as EN 16798-7:2017 focuses on the calculation of the building energy use in periods when there is a cooling demand, and they have not been checked for very small temperature differences.

·         Cp coefficients used in this study are the ones provided in (Liddament 1996), where other sources provide other values.

·         The airflow rates only apply when windows are open. In case of high-speed winds or high temperature differences, when windows may only be open for very short periods of time, the averaged airflow rate may not be relevant.

Acknowledgements

The authors would like to thank VELUX A/S for funding this study.

References

Larsen, Tine Steen, Christoffer Plesner, Valérie Leprince, François Rémi Carrié, et Anne Kirkegaard Bejder. 2018. « Calculation Methods for Single-Sided Natural Ventilation: Now and Ahead ». Energy and Buildings 177 (October): 279‑89. https://doi.org/10.1016/j.enbuild.2018.06.047.

Leprince, Valérie; Carrié, François-Rémi. s. d. « Comparative analysis of window airing models proposed in prEN 16798-7 and influence of internal resistances ». In CLIMA 2016 - proceedings of the 12th REHVA World Congress: volume 5. Aalborg: Aalborg University, Department of Civil Engineering. Aalborg University, Denmark.

Liddament, Martin W. 1996. A Guide to Energy Efficient Ventilation: This Report Is Part of the Work of the IEA Energy Conservation in Buildings & Community Systems Programme, Annex V. Coventry: Annex V. Air Infiltration and Ventilation Centre.

Endnote