Stay Informed
Follow us on social media accounts to stay up to date with REHVA actualities
Marko G. IgnjatovićUniversity in Niš, |
Bratislav D. BlagojevićUniversity in Niš, |
Mirko M. StojiljkovićUniversity in Niš, |
Dejan M. MitrovićUniversity in Niš, |
Aleksandar S. AnđelkovićUniversity of Novi Sad, |
Energy consumption in buildings is one of the top priorities in official
energy policies of many countries. The main reason behind this lies in the
significant increase in energy consumption in the building sector. According to
Perez-Lombard [1], buildings accounted for more than 37% of the final energy
consumption in EU during 2004, with a similar situation present in the USA
where in 2010 buildings participated with more than 40% of primary energy
consumption [2]. Gruber [3] points out that 50% of the energy consumed in buildings
in industrialized countries is used for heating, ventilation and
air-conditioning. The situation is almost identical in Serbia, where the building
sector participates with more than 50% of the consumed energy [4].
Energy consumption in buildings can be reduced by a number of energy
efficiency measures, with the most frequent being: improving the building
envelope thermal characteristics, using energy efficient HVAC equipment, and employing
renewable energy sources. What is common for all these measures is that they
are implemented during the refurbishment of existing buildings or the construction
of new buildings, and that in the majority of cases it is legally regulated
[5]. Recently, strong research efforts have been put in to improve building
energy performance without major renovations of buildings/systems, but just by
improving the existing systems and incorporating new automatic regulation
concepts [6–8]. This primarily relates to the minimization of energy
consumption/energy cost/GHG emissions in buildings while maintaining the thermal
comfort of occupants within the desired range. The basis for this kind of
research are the mathematicsl models of buildings and related systems. Modeling
and prediction of performance focus on three categories [9]: long-term load
forecasts for system selection and planning; medium-term forecasts for system
maintenance and fault detection and diagnosis; and short-term forecasts for
daily operation, scheduling and load-shifting plans.
Models of buildings and their accompanying systems for short-term forecasts
are as follows: white-box models, black-box models, and gray-box models. White-box
models include physical characteristics and relations of buildings and their
systems, and are incorporated in the best-known building dynamic simulation
programs such as: EnergyPlus [10], TRNSYS [11] etc., and are of special
interest for this research.
The optimization process can be repeated time after time, resulting in the
moving horizon optimization implemented in numerous studies on the topic of
model predictive control [12–16].
This paper presents the possibility to minimize building energy
consumption by optimizing the existing HVAC system operation modeled in
EnergyPlus, while maintaining the occupant thermal comfort at the same time.
The planning horizon is set to one day assuming a perfect weather forecast, and
the optimization process is repeated day-by-day in the observed period.
The optimization process is based on the combination of detailed hourly
simulations of the building performed in EnergyPlus and the operation
optimization of selected HVAC systems developed in the C# programming language.
The optimization process follows a relatively simple iterative procedure described
in [9].
The optimization problem is solved by using the parallel particle swarm
optimization (PSO) [17].
The program starts by loading the building model and weather file. The
building energy model created in EnergyPlus contains all the information on the
analyzed building, and it is, basically, a text file with the values in
particular lines which the optimization algorithm will replace with the values
of selected decision variables. At the beginning of each iteration, the program
randomly generates a population of decision vectors and creates as many text
files as there are vectors. The program initiates the simulation of all files
related to a current PSO iteration, and all simulations are carried out simultaneously.
After all the simulations have finished, the program reads the resulting output
files and extracts the values required to calculate the objective function
value(s). The objective function can be easily defined according to a
particular interest. The process is then repeated in a new iteration, with a
new population of decision variable vectors randomly generated around an
optimal vector of the last completed iteration. This process repeats until the exit
criteria is fulfilled.
When the exit criteria is satisfied, the optimization process is repeated
for the next optimization period (part of day, one day, several days, etc.).
The case studied in this paper is the office part of the Feniks BB Company
building in Niš, Serbia (Figure 1). The building is a combination of the office and
manufacturing type.
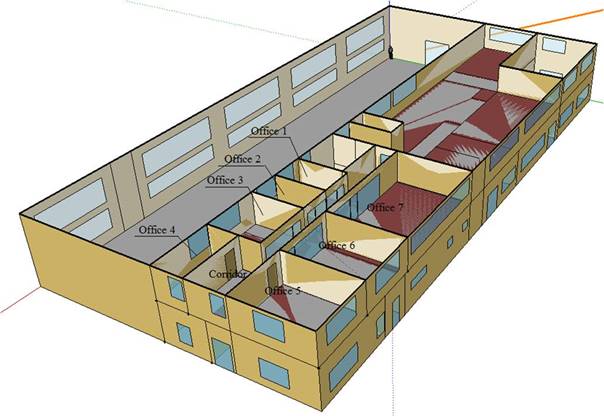
Figure 1. Office part of the
building.
The building is located on the outskirts of Niš, the largest city in
Southeast of Serbia. The useful floor area of the building is 1630 m². One
part of the building, approximately a half, represents a manufacturing hall,
while the other part is divided into two stories. The lower storey houses
manufacturing premises and warehouses, while the upper storey is where offices and
manufacturing of electronic components are located.
The building is mainly heated by radiators and air heaters (the manufacturing
hall), while the office part of the building can also be heated by a ducted
fan-coil unit with 100% of fresh air which at the same time presents the basic cooling
system in the said space. The AHU consists of the following sections:
air-to-air plate heat exchanger for heat recovery, coil section (cooling or
heating as necessary), fan sections, and sound attenuators. The air conditioning
system is designed in the classical manner to ensure the indoor temperature for
a summer design day. The operation of all secondary systems is controlled by
PLCs.
Gas-fired condensing boilers and air-to-water heat pump are used as the primary
energy sources.
The simulation program EnergyPlus was used to create the building model and
the mentioned HVAC systems. The building geometry was created using the Open Studio Plug-in for Google SketchUp. All rooms in the building were
treated as separate thermal zones.
To simulate the building, an appropriate weather file containing all
boundary conditions was also needed. A custom weather file in was formed from
the data provided by the hydrometeorological station Niš.
The offices were assumed to be occupied during weekdays from 08:00 to 17:00
(the last occupied hour is from 16:01 to 17:00), with a number of occupants
occupying them as defined in Table 1. The aim is to
maintain thermal comfort within the prescribed range by optimizing the HVAC
system operation day by day. As the indicator for thermal comfort the predicted
mean vote (PMV) was used, and this value could be generated as the output from
the simulations on an hourly basis for every modeled zone. Even though the
outputs for PMV are expressed on a discrete scale from −3 to +3, the
EnergyPlus algorithms carry out the calculations on a continuous scale which is
not an error [18], and the value of PMV obtained through simulation can be
treated as the one which meet or does not meet the desired value (e.g. PMV can have
the value of 0.23784, so if the desired comfort value is 0.5, this means that
the comfort is satisfied in the given hour).
Table
1. Typical number of occupants in offices during weekdays.
Thermal
| Number of |
Office 1 | 2 |
Office 2 | 2 |
Office 3 | 2 |
Office 4 | 2 |
Office 5 | 1 |
Office 6 | 4 |
Office 7 | 4 |
Corridor/lobby | 2 |
The period starting
on January 27th 2014 and ending on February 6th 2014 was selected to meet the needs of this paper and check the
methodology. A weather file in the appropriate format was created on the basis
of the data provided by the Republic Hydrometeorological Service of Serbia – the
hydrometeorological station Niš.
The optimization period of one day was adopted, and the optimization process
itself was performed for each day of the stated period including weekends,
which were treated as a single optimization period.
To perform the optimization task and calculate the objective function,
decision variables should be defined first. Since the optimization goal is to
achieve the minimum primary energy consumption while maintaining the thermal
comfort for one day, having the simulation tool limitations in mind, variables
were classified into two groups: the ones which can be modified hourly/daily
and the others which can be modified once per simulation. Certain variables were
further subdivided into three periods of day for each day in the observed
period: unoccupied before occupants arrive (from midnight to 08:00); occupied
period (from 08:00 to 17:00); unoccupied after occupants leave (from 17:00 to
midnight). To reduce the total number of decision variables, only one decision
variable for each of the unoccupied periods was allowed. Furthermore, some
decision variables were constrained by the fact that the system was already
installed and there were limitations especially in terms of capacity and maximum
flow rates.
For the observed winter operation, the following variables were adopted:
·
Hot water supply temperature (hourly with distinction between
occupied and unoccupied periods) - 13 variables within range 40–70°C;
·
Heating set-point for offices served by baseboard heaters
(hourly with distinction between occupied and unoccupied periods) - 13
variables within range 18–24°C;
·
System air flow rate (once per simulation) - 1 variable
within range 0.5–1.2 m³/s ;
·
Minimum outside air fraction (hourly) - 24 variables within
range 0.6–1;
·
Baseboard heaters runtime (daily) - 1 variable;
·
Baseboard heaters finish time (daily) - 1 variable;
·
Heat Recovery runtime (daily) - 1 variable;
·
Heat Recovery finish time (daily) - 1 variable;
·
Heating Coil runtime (daily) - 1 variable;
·
Heating Coil finish time (daily) - 1 variable;
·
Heat Recovery bypass minimum limit temperature (once per
simulation) - 1 variable.
Since two different HVAC systems (radiator heating and air-conditioning
system) were served by the same heat source, using a built-in energy management
system of EnergyPlus, a syntax was created according to which the heat source (boiler)
was available whenever either of the two systems was required. A similar syntax
was created for the AHU supply and exhaust fans, depending on whether the
heating coil and/or heat recovery were needed.
The objective function of the optimization problem is given in the form:
| (1) |
subject to:
| (2) |
where E represents the
primary energy consumption from the systems; EB [kWh] is the
boiler energy consumption; ESF [kWh] is the supply fan
electricity consumption; ERF [kWh] is the return fan
electricity consumption; 1.1 is the primary energy conversion factor for
natural gas; 2.5 is the primary energy conversion factor for electricity;0.5 is the boundary value of PMV, and TCF is the thermal comfort related function in the form:
| (3) |
In equation 3, i represents the
zone identifier; minPMViis the minimal value of PMV in the i-th zone; Ni is the number of occupants in
the i-th zone; Ntot is the total number of occupants.
The values of EB, ESF, ERF and PMVare the outputs
from EnergyPlus simulations.
For the PSO algorithm, the population size was set to 1000, while the number
of generations was set to 50. The exit criteria were not defined, meaning that
all 50,000 simulations were performed.
The simulations were run on a 24-core Intel Xeon working station with 32GB
of RAM memory. The optimization process was run for every weekday of the
observed period and also for the weekend but with less strict criteria for TCF.
The optimization lasted between 22 and 24 hours, meaning that there was enough
time left to implement the optimal decision variables vector into the existing
automatic regulation system, assuming that the weather forecast for that
particular day was perfect.
To compare the results obtained in the optimization, a baseline case was
adopted. This case represented the usual operation of the existing HVAC systems.
The main differences between the baseline and the optimal model were:
·
in the baseline case, the given thermostat values for all
zones were predefined with constant value setpoints (18/20/22°C during the
occupied period depending on the part of the building), while in the initial
models, the thermostat values in the office part of the building were varied
(in the remaining zones of the model the values are the same as in the baseline
model),
·
the systems were turned on in a predefined manner - 1 hour
before the occupants arrive (AHU was turned on during the occupied period only),
and remained on for the entire occupied period of day, while in the initial
models these could be turned on any time if necessary,
·
in the baseline case the heating supply temperature was dependent
on the outdoor temperature, while there was no such dependency in the initial
models,
·
during the weekend there were no occupants, thus the systems
remained turned off in the baseline model, while in the optimized model the systems
might be run in order to provide good initial values for the first day
following the weekend.
In the baseline case, the primary energy consumption had the value of
3451.2 kWh for the analyzed period, out of which 3232.6 kWh was for
space heating (baseboards, unit ventilators and heating coil), and 218.6 kWh
was for electricity for running the AHU fans. The PMV values in the offices are
shown in Figure 2.As it can be seen, the PMV
value in every zone was not even near the threshold value of −0.5. For
the optimized case (the optimal values from each day joined into a single
simulation), the primary energy consumption had the value of 4024.9 kWh,
and was used only for space heating, meaning that there was no need to turn on
the AHU. The increased energy consumption was due to the weekend operation of
the systems and resulted in 618.2 kWh of primary energy consumption. Thus
increased energy consumption resulted in a much better occupant thermal comfort
in all zones as shown in Figure 3.
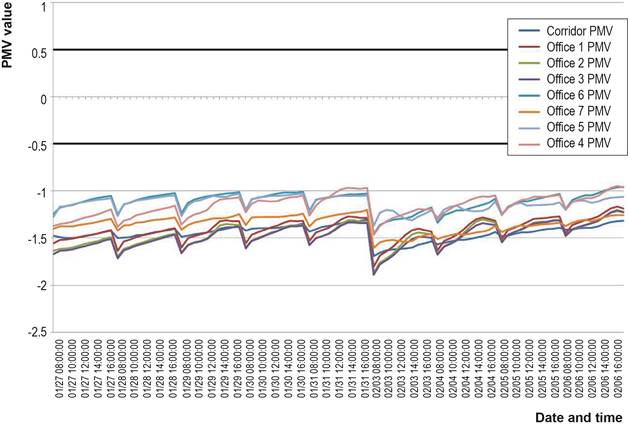
Figure 2. PMV variation in
offices - baseline case.
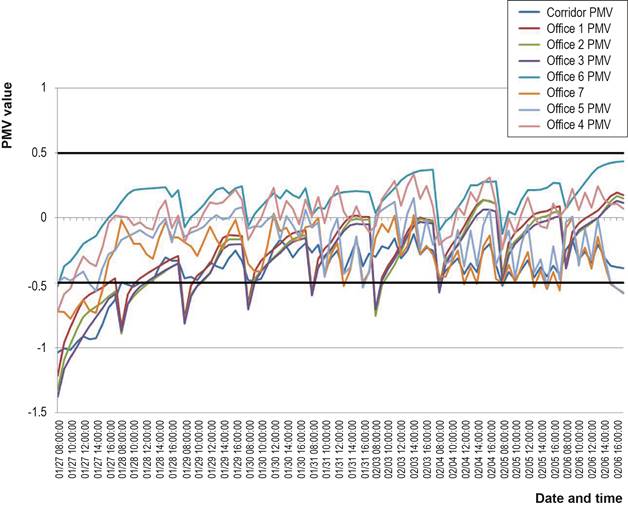
Figure 3. PMV variation in
offices - optimized operation.
It is interesting to note that for the optimal case no correlation could
be made between the heating supply temperature and the outdoor temperature (Figure 4), which can potentially represent the material for future
research with the aim of finding the heating curves with which system operators
are familiar.
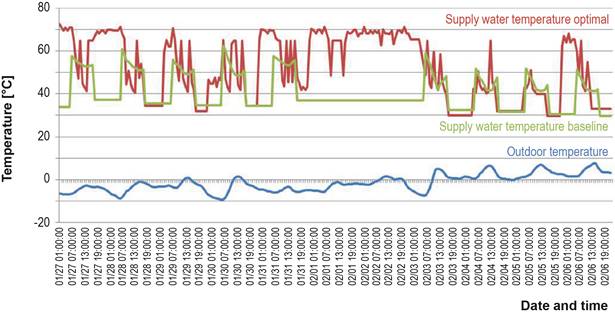
Figure 4. Heating supply temperature variation.
This paper presents the possibility to
minimize primary energy consumption in offices by implementing the optimized operation of the existing HVAC
systems, while simultaneously maintaining the thermal comfort of occupants
within the desired range. The main goal of the paper was to show that with the
existing HVAC system designed in the traditional manner, users or system
operators can define in advance the thermal comfort level which the system will
try to meet with minimal energy consumption. The main advantage of this
methodology is that it can be applied with relatively small modifications of
the existing HVAC system. Future research will be dedicated to the moving
horizon approach and the implementation of the obtained optimal values into a
real system, as well as their experimental verification. In addition, decision
variables and objective function need to be checked in order to generalize the
application of the presented process.
The authors are particularly grateful to the Republic Hydrometeorological
Service of Serbia, Observatory in Niš for providing the weather data in order
to conduct this research, and to the company "Feniks BB" d.o.o Niš for their support in helping record building operation
and install additional measuring equipment.
[1] Perez-Lombard,
L., J. Ortiz, C. Pout, A review on buildings energy consumption information, Energy
and Buildings, 2008, Vol. 40, pp. 394-398.
[2] 2010 Buildings energy data book, Office of energy efficiency and
renewable energy, US Department of Energy, 2011. [accessed 12.09.2015]
[3] Gruber, M., A. Truschel, J.O. Dalenback, Model-based controllers
for indoor climate control in office buildings– Complexity and performance
evaluation, Energy and Buildings, 2014, Vol. 68, pp. 213-222.
[4] Bojić, M., N. Nikolić, D. Nikolić, J.
Skerlić, I. Miletić, A simulation appraisal of performance of
different HVAC systems in an office building, Energy and Buildings, 2011, Vol.
43, pp. 1207-1215.
[5] Ordinance on Energy Efficiency of Buildings, Republic of Serbia
Ministry of Environment, Mining and Spatial Planning,Official Journal of the Republic of Serbia
(in Serbian), 61/2011.
[6] Afram, A., F. Janabi-Sharifi, Theory and applications of HVAC control
systems - A review of model predictive control (MPC), Building
and Environment, 2014, Vol. 72, pp. 343-355.
[7] Lazos, D., A. Sproul, M. Kay, Optimisation of energy management in
commercial buildings with weather forecasting inputs: A review, Renewable and
Sustainable Energy Reviews, 2014, Vol. 39, pp. 587-603.
[8] Shaikh, P.H, N.B.M. Nor, P. Nallagowden, I. Elamvazuthi, T.
Ibrahim, A review on optimized control systems for building energy and comfort
management of smart sustainable buildings, Renewable and Sustainable Energy
Reviews, 2014, Vol. 39, pp. 409-429.
[9] Li, X., J. Wen, Review of building energy modeling for control
and operation, Renewable and Sustainable Energy Reviews, 2014, Vol. 37, pp.
517-537.
[10] EnergyPlus
- Energy Simulation Software,
http://apps1.eere.energy.gov/buildings/energyplus/
[11] TRNSYS -
Transient System Simulation Tool, http://www.trnsys.com/
[12] Coffey, B., F. Haghighat, E. Morofsky, E. Kutrowski, A software
framework for model predictive control with GenOPT, Energy and Buildings, 2010,
Vol. 42, pp. 1084-1092.
[13] Ma, J., J. Qin, T. Salsbury, P. Xu, Demand reduction in building energy systems
based on economic model predictive control, Chemical
Engineering Science, 2012, Vol. 67, pp. 92-100.
[14] Zhao, J., K. Poh Lam, B. Ydstie, Energyplus model-based predictive control
(EPMPC) by using MATLAB/Simulink and MLE+, Proceedings of
BS 2013 - 13th Conference of International Building Performance Simulation
Association, IBPSA,
Chambery, France, 2013.
[15] Zakula, T., P.R. Armstrong, L. Norford, Modeling environment for model predictive
control of buildings, Energy and Buildings, 2014, Vol. 85, pp. 549-559.
[16] Hussain, S., H. Gabbar, D. Bondarenko, F. Musharavati, S. Pokharel,
Comfort-based fuzzy
control optimization for energy conservation in HVAC systems, Control Engineering Practice, 2014, Vol. 32, pp. 172-182.
[17] Rao, S.S., Engineering Optimization: Theory and Practice, John
Wiley & Sons Inc., New Jersey, USA, 2009.
[18] ***,
EnergyPlus Engineering reference, DOE, 2015.
Follow us on social media accounts to stay up to date with REHVA actualities
0