Optimizing self-consumption of grid-connected PV/storage systems

This article is based on the paper of the winner of the student competition organised during the World Sustainable Energy Days in Wels, Austria in February 2014

An electrical storage system is mainly used to increase self-consumption of the produced photovoltaic energy, relieve the public power grid and to reduce the dependency on the grid. This article focuses on a technical simulation of a photovoltaic (PV) system linked to a storage unit and analyses its economic efficiency.

Electricity is accepted as one of the driving forces for economic development around the whole world. Nowadays the human population depends on fossil fuels like oil, gas and coal for electricity production. Two major disadvantages are the depletability of these fossil resources and the resulting carbon dioxide emissions when burning them.

To reduce the energy demand and fossil fuels the following core actions need to take place in the order shown below:

·  Energy savings

·  Energy efficiency

·  Supply of renewable energy sources

In the course of time the subsidies for private customers have been decreasing and the costs for electricity per kWh have been continuously rising. As a consequence, especially grid connected photovoltaic systems increased substantially over the past few years [1] resulting in commercial sales of energy to the distribution network if there is any surplus of PV energy. To make these systems economically viable without funding, it is necessary to use as much self-generated PV electricity [2] as possible by the directly connected consumers themselves – this factor is described by the self-consumption (SC) rate [3].

The integration of a storage system

The proper sizing and the correct configuration of the individual parts of the home power plant (load, solar yield and storage) are crucial for the cost-efficient operation [4]. In this context it is important not to oversize the storage system, because the investment costs would be enormous and subsequently the system would not be profitable.

The lifetime can be maximized by the correct operational management of the system. One important point of this consideration is the storage strategy. For the simulation a simple model has been designed:

·  Energy is supplied by the PV system and there is an energy demand in the household, the energy is used by the household itself.

·  If the energy produced by the PV system is higher than the currently required demand of the household, the surplus is stored.

·  If more power is required than provided by the PV system at the moment, energy is taken from the battery.

·  Energy is only taken from the public power grid if the demand of the household cannot be met by the storage system.

·  If there is neither a demand nor a free storage capacity, the surplus is fed into the public power grid.

This model for charging and discharging the battery is not a strategy in the proper sense. Storage strategies for example take into account weather forecasts and foreseeable loads to properly manage available capacity in the storage. Furthermore the addition of a charge control, an overcharge protection and a deep discharge protection is important to increase the lifetime of the electrical storage system [5].

One of the reasons why it will be necessary to implement a storage strategy is shown in Figure 1. The frequency distribution of the storage state (empty of full) is recorded for each month with the associated percentage of the average state of charge. According to the simulation in January the battery is empty 81% of the time.

This means the capacity sinks to the maximum depth of discharge (DoD) and the battery just works 10% of the time in the first month of the year. Considering the months May to July the two bars are almost equal. The battery is full 40% of the time in summer because of the high solar yield and therefore the working time is also reduced.

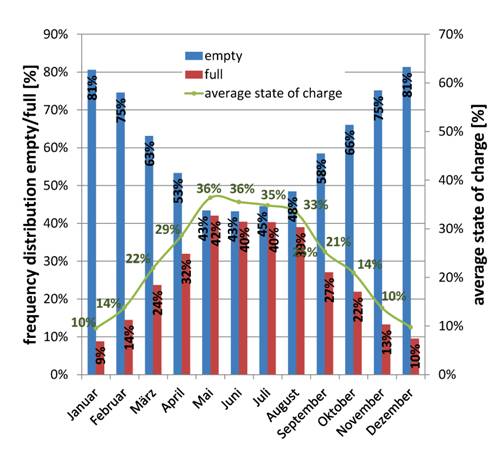
Figure 1. Frequency distribution of empty and full in a 2 kWh storage in comparison with a 5 kWp PV plant.

In a theoretically perfect operation the two bars would approach zero. In reality this cannot be reached: a small battery in winter is empty most of the time and full in summer. This is because of the low capacity of the battery and thus it is quickly loaded, respectively unloaded.

In comparison, a big storage system is often full and hardly empty in summer (kind of seasonal storage). This damages the battery because there is no full load cycle over a longer time.

PV/Storage Simulation

The available capacity of the battery consists of the depth of discharge, the maximum charge and the efficiency of the battery. Within the course of the simulation the charge and discharge efficiency are not taken into consideration. The cycle stability is closely linked to the life-time of a battery. This value is significant for the annual complete charge cycles. The size of the exemplary household is based on data from “STATISTIK AUSTRIA” [6] and is rounded to 4000 kWh/a.

The same principle is used to calculate the self-consumption rate with an integrated battery system. Figure 2 shows the self-consumption rate by varying the PV plant size and the available battery capacity.

The higher the battery capacity, the greater the self-consumption rate because more surplus energy can be stored. The sum of the self-consumption rate and the amount of energy fed into the public grid and also the sum of the solar coverage rate and the energy obtained from the public grid always equals 100%.

Figure 2.Self-consumption in cause of the combination of PV and storage system.

It might appear that an increase in battery capacity will continuously lead a proportional increase in the self-consumption rate. However, Figure 3 clearly shows that at a particular value the increase of the curve slows down. Therefore a supersized storage would be necessary to achieve 100% of self-consumption rate.

Pros and cons must be carefully considered when choosing the size of the electric storage system. Small batteries have the advantage of being less expensive, but on the other hand they are not able to store the midday peak energy input of a sunny day and to cover the evening demand of a household because of the low capacity.

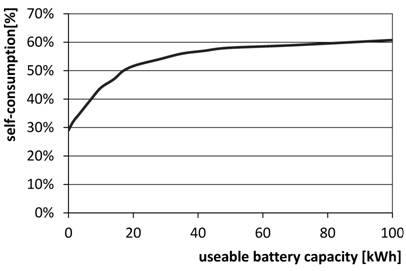
Figure 3.Self-consumption in the case of variable battery and an exemplary household (4000 kWh/a) with a 5 kWp PV.

To choose a suitable storage system all major factors need to be taken into consideration. These include the household with the specific load profile, the photovoltaic yield depending on the location, the direction of the photovoltaic modules and the efficiency of the inverter and the storage system. Only with a suitable storage system, the self-consumption rate can be increased significantly and consequently the profitability of the system is given.

In order to achieve a higher rate of self-consumption, higher storage capacities are needed. In this case the system will not be amortized in the lifespan of the PV power plant assuming of real specific costs of a battery system of at least 300 €/kWh for lead batteries and 500-1000 €/kWh for lithium batteries [7].

Economic Assessment

As basis for the economic calculation of the exemplary household a storage system with a 5 kWh useable battery capacity (including DoD and the efficiency of the system) was used. For the simulation are network costs of 22 €ct/kWh, a feed-in tariff of 5.5 €ct/kWh and an estimated 2% increase in electricity prices per year [8] assumed.

The Lithium battery with specific costs of 500 €/kWh is not amortised within 25 years. By only changing the increase in electricity prices per year to 4% the complete system is being amortized within 22 years. This means even a small change in the underlying assumptions causes a significant change in the results.

The result of the economic assessment of an electrical storage system is shown in Figure 4. A Lithium battery with a varying capacity between 2 and 150 kWh in combination with a PV plant size of 5 kWp and an annual electricity consumption of 4000 kWh/a is illustrated. The green area in the left corner highlights an amortisation time of more than 25 years.

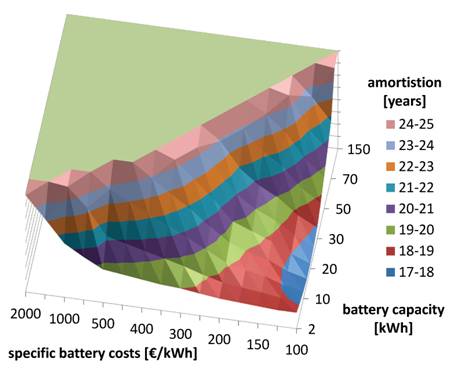
Figure 4.Amortisation of a Lithium battery in combination with 5 kWp PV and 4000 kWh/a.

This calculation does not include subsidies and new storage acquisition. In realty the storage system should be replaced every 5 to 15 years due to capacity losses depending on the storage technology and the operation of the system. This means, based on a typical 25 year lifespan of the PV system, the storage system has to be renewed three to five times.

Compared with the specific grid costs per kWh shown in Figure 5 the electricity costs for combined PV and battery the point of intersection is reached after 24 years. This means that after 24 years the costs for the PV/storage system are as high as the sum costs over the years of the public grid. Without a battery system the point is reached after 18 years.

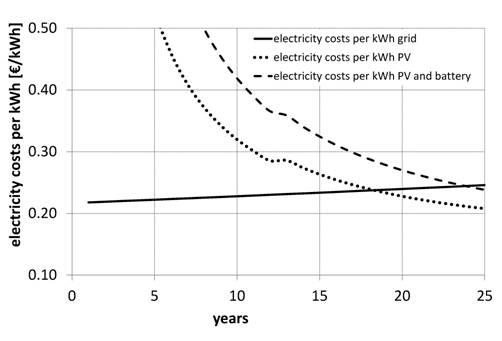
Figure 5. Electricity costs per kWh.

In conclusion the amortisation of a storage system depends on the photovoltaic plant size, the load profile of the household and the electrical storage system itself.

Conclusions

In this paper simulations to increase self-consumption with a grid-connected PV power plant are illustrated by calculation of an exemplary household. To further increase the level of self-consumption rate and the profitability of the system, the PV system can be combined with a storage system. As a result the surplus energy of the PV power plant can be stored in the battery and discharged again when energy is needed.

The battery was selected based on the following criteria:

·  Depth of discharge

·  Lifetime

·  Self-consumption

·  Investment costs

·  Payback period

There are many new battery technologies under development and in the next few years the price per kWh is expected to drop significantly so that the system can be economically viable within the lifespan of the PV plant.

The mentioned parameters (self-consumption rate and solar-coverage rate) can reach 100% but major efforts will have to be made to reach this maximum and it may not be economically attractive. The aim is to find a balance between optimization of the parameters and the reduction of expenses for the system.

The actual behaviour of the user has a major influence on the self-consumption rate. An identical load profile but different annual energy consumption shifts the curve (bigger consumption means higher self-consumption). It turned out that currently an electrical storage system for households only in a few cases is economically viable and energetically appropriate.

Acknowledgements

This article is based upon work, carried out within the cooperative research project “Vision Step I” (smartcityvillach.at). This project is funded by the Austrian Climate and Energy Fund within the program “SMART ENERGY DEMO – FIT for SET”.

References

[1]     V. Quaschning, Regenerative Energiesysteme - Technologie, Berechnung, Simulation, München: Hanser Verlag, 2013.

[2]     A. Einfalt, C. Leitinger, D. Tiefgraber and S. Ghaemi, “ADRES Concept – Micro Grids in Österreich,” Wien, 2012.

[3]     J. Kathan and M. Stifter, “Increasing BIPV self-consumption through electrical storage - feasible demand-coverage and dimensioning of the storage system,” 5th International Renewable Energy Storage Conference IRES 2010, Berlin.

[4]     G. Mulder, F. De Ridder and D. Six, “Electricity storage for grid-connected household dwellings with PV panels,” Solar Energy, pp. 1284-1293, 2010.

[5]     A. Jossen, J. Garche and D. U. Sauer, “Operation conditions of batteries in PV applications,” ScienceDirect, 2004.

[6]     S. Manuela, “statistik austria,” Mai 2013. [Online]. Available: http://www.statistik.at/web_de/dynamic/statistiken/energie_und_umwelt/071019. [Accessed 30 September 2013].

[7]     D. U. Sauer, “Dezentrale Energiespeicherung zur Steigerung des Eigenverbrauchs bei netzgekoppelten PV-Anlagen,” Aachen, 2011.

[8]     PV-Austria, “PV-Austria,” Photovoltaic Austria Federal Association, 2013. [Online]. Available: http://www.pvaustria.at/. [Accessed 25 September 2013].