Stay Informed
Follow us on social media accounts to stay up to date with REHVA actualities
|
Livio Mazzarella |
Department of Energy, Politecnico di Milano, Milanlivio.mazzarella@polimi.it |
COVID-19 pandemic is today an unresolved medical problem and any possible measure that may lower SARS-CoV2 virus propagation has to be applied. While the medical research area is still learning about how the virus spreads and the severity of illness it causes, and there is no unanimous consensus on the airborne infection route, starting from this today even more recognised possibility, the engineering research area is working to produce guidelines focusing on how to reopen and safely use buildings after the lockdown, providing advice on specific components, buildings/space types, and suggesting mitigation measures [1].
If airborne viral emission and diffusion are assumed to be important, there are several design and operational measures that can be undertaken for reducing the airborne infection risk in closed spaces as buildings:
· ventilation rates should be increased as much as compatible with comfort and energy issue;
· indoor air and extracted air should not be recirculated;
· individuals should avoid staying directly in the flow of air from another person;
· the number of people sharing the same indoor environment should be minimized, and last resort;
· people working/studying/etc. in a common space should correctly wear protective facial masks.
Effects on virus spread of all these measures are not easily quantifiable, but for some of them some simple modelling can help to understand their relative effectiveness. For this reason, a simplified tool has been developed to assess comparatively effectiveness and potential application of such of actions on both existing and new building and HVAC systems.
The tool is based on the standard airborne disease transmission Wells-Riley model, i.e. quanta based and full mix hypothesis behind, described in [2] and [3]. It extends the single room model to a Multi-rooms Model with possible air recirculation among rooms, through centralised HVAC system and via air transfer to common service area (corridor, toilettes and staircases) where air extraction to outside is performed via dedicated exhaust air ductwork. The model is a dynamic model, i.e. the time dependent problem is solved.
It is possible to partially remove the full-mix hypothesis using the ventilation Contaminant Removal Effectiveness, ϵr, which depends on the chosen air distribution system. In the tool it is possible to modify the recirculation ratio from 1 to 0 and eventually to add an HEPA filter or equivalent virus removal/inactivation equipment (UV-C, etc.) on the return air lo lower as much as possible the virus spread via air recirculation. The model also accounts for “virus losses” in the HVAC system (deposition in ducts, in AHU and natural decay when contaminated air moves through such components), using the same approached used for rooms but in steady state approximation, i.e. using virus removal coefficients as done for general spaces.
Splitting the ductwork in supply and return branches, which can have significant different virus concentrations, and using a volume weighting factor to account for the different pathways different virus concentrations have to go through before to reach the AHU or to reach each served spaces, under Quasi Steady State Hypothesis the concentration balance equation on the returnductwork can be rewritten for each branch i as:
(1) |
where
CETA,i is virus concentration in extracted air at the end of specific ductwork branch from Room i to AHU, in [quanta/m³];
Cavg;i is average virus concentration in this ductwork branch air volume, [quanta/m³];
λRd,d,i duct virus removal coefficient for ductwork serving Room i, [h-1];
VRd,i volume of return ductwork serving Room i, in [m³];
qV;ETA,i extracted volume air flow from Room i, in [m³/h].
with
(2) |
where
λR,d,i virus removal coefficient by deposition on surfaces of ductwork serving Room i, [h-1];
κR,i virus decay coefficient of ductwork serving Room i, [h-1];
λR,ad,i virus removal coefficient by additional measurements of ductwork serving Room i, [h-1];
Assuming linear approximation
(3) |
it is
| (4) |
where
αR,i dimensional removal factor for return branch i, in [h];
βR,i dimensionless removal factor for return branch i, [−] defined as
![]() .
.
Air Handling Unit is modeled using same approach after mass conservation balance is applied to the system described by Figure 1, where an air dumper is controlling the recirculation ratio (RF).
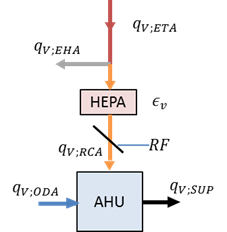
Figure 1. Recirculation managed by AHU with removal/deactivation device on the return duct after exhaust air expulsion.
The input to the removal/deactivation device, identified as HEPA filter in Figure 1, is the weighted virus concentration in the extracted ait from each room as
| (5) |
Thus, the recirculated air virus concentration before mixing with outdoor ventilation air is
| (6) |
where ϵvis the removal/deactivation device efficiency, [−], and the supply air virus concentration is given by:
| (7) |
where
CODA (t) virus concentration in outdoor air, in [q/m³], usually null;
RF UTA recirculation factor, in [−]; defined as RF = qV;RCA /qV;SUP
Thus, under Quasi Steady State Hypothesis, the virus concentration balance over the AHU as black box is written as for the ductworks as:
| (8) |
where coefficients λUTA, αUTAand βUTA have the same meaning as expressed before for the return ducts.
Under Quasi Steady State Hypothesis, the concentration delivered by each supply ductwork branch i can be written as for the return ductwork as:
| (9) |
where λSd,d,i is the duct virus removal coefficient for ductwork supplying Room i, [h-1];
Combining equations from (1) to (8), assuming null the virus concentration in the outdoor air, the virus concentration in the supply air to each room can be written as function of the virus concentration in each room:
(10) |
where the dimensionless virus removal factors βS,i, βUTA and βR,k account for virus removal due to deposition and decay in the ductworks and AHU, while ϵv is the efficiency of the virus removal/inactivation unit.
For the generic Room i, the concentration balance in full mix hypothesis is
| (11) |
where
Ċs,i virus concentration source in Room i, in [q/(h m³)],
γi virus supply coefficient in Room i due to recirculation, [h-1].
λi virus total removal coefficient in Room i, [h-1].
To account for specific flow pattern due to air distribution system typology and thus partially remove the full mix hypothesis, the virus supply coefficientγi is defined as:
(12) |
where
qV;SUP,i supply air volume flow rate to Room i, in [m³/h];
ϵr,i ventilation Contaminant Removal Effectiveness Room i, (=1 for full mix), [−];
Vi volume of Room i, in [m³].
To account for facial mask effect on virus spread by the infected person, the virus concentration source is defined as
(13) |
where
ei virus emission rate per person in Room i, in [q/(h pers)];
IPi number of infected people in Room i, in [pers]
ϵIPFM,i facial mask efficiency for infected person in Room i, [−].
Instead, the effect of facial masks worn by susceptible people is taken into account when calculating the infection risk probability using the Wells-Riley model, i.e.
| (14) |
where
ϵSPFM,i facial mask efficiency for susceptible people in Room i, [−].
IRi present people breathing rate in Room, in [m³/h];
tex,i exposure time (given space occupancy time interval) in Room, in [h]
Cavg,i average virus concentration in the given space over the occupancy time interval, in [q/m³].
The average number of potentially infected people is then given in each room by
(15) |
where
NPi number of people in Room i, [pers];
IPi number of infected people in Room i, in [pers].
Combining equation (10) with equation (11) it is possible to write for each room ian ordinary differential equation like
(16) |
which can be approximated by an algebraic equation substituting the time derivative with a forward finite difference obtaining
(17) |
where
∆t is the discretization time interval, in [h];
ai,j coupling coefficients, in [h-1];
![]() virus
source term, in [q/(h m³)];
virus
source term, in [q/(h m³)];
τ integer time index (t = τ · ∆t), [−].
Equation (16) represents a set of N equations that can be easily solved using matrix notation as
(18) |
where
| (19) |
NOTE: to have a fast-to-solve problem fixed air flow rates over the whole calculation day are assumed; this assumption implicates constant coefficient for the matrix equation (18), but does not change the model structure, which can account for variable flows calculation (if air flow time schedule are provided as input) just updating the matrix coefficient each time step.
To have a relatively easy and fast to use tool some limitations have been applied as
· constant ventilation air flow rate during the whole day;
· fixed building plan layout typology to allow fast data input and calculations (see Figure 2);
· rooms number is unlimited (memory space is just sized to manage 100 rooms, but can be expanded according to the available computer memory), while there is only one corridor, one toilet and one staircase compartment;
· extraction-only systems are possible in toilets and staircase only;
· transferred air through the corridor is automatically calculated, if any exists due to extraction in toilets and/or in staircase compartments;
· virus source (infected person) can be placed in any place and can be more than one, each with its specific virus strength.
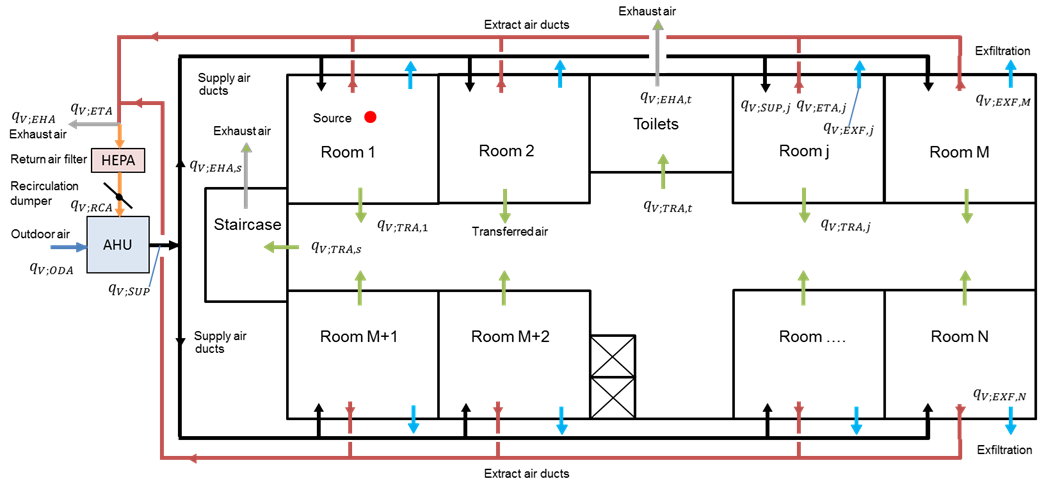
Figure 2. System layout.
The basic assumption to use the tool is that all supply and extracted air flow rate to/from each room are known and the extracted flow rate is provided as a fraction of the supply one. These parameters are usually provided in the system design masterplan.
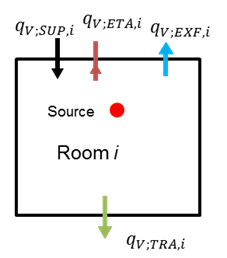
Figure 3. Air mass balance in Room i.
To avoid to solve an air flow network, a simplified approach is then used to calculate transferred air flows, which are allowed only between rooms and corridor, and corridor to toilets and/or staircase if any exhaust air extraction is in place there. The basic assumption is that any room is always in pressurized state, i.e. only exfiltration and transferred air flows are allowed (Figure 3). An air mass balance on the whole system is then performed to calculate transferred air flows assuring air mass conservation consistency.
Input checks are employed as well as mass balance check to avoid that some inconsistent input is producing inconsistent result.
An occupancy schedule can be specified only with to time slots inside the building operational time in a day (the tool calculates for one day only), but it can be different in any room.
As result of the tool calculation the following data are available in the main sheet of the Excel workbook (Multi-cal):
· average virus concentration in each room, corridor, toilettes and staircase, over the working day, in quanta/m³;
· individual infection risk over the day in each of those spaces calculated with the Wells-Riley model, in [%];
· average number of potentially infected people in each room, corridor, toilettes and staircase, over the working day;
· virus air to surface deposition over the day in each space, on AHU surfaces, on HEPA or equivalent equivalent virus removal/inactivation equipment (V-C, etc.), on supply and return ductworks, in quanta.
The virus concentration time evolution in each space is reported (using a printout time interval, which can be greater than the integration time interval) in a second sheet called “Concentrations”, while air to surface virus deposition time history is available in a third sheet called “Depositions”.
In the main sheet diagrams, see Figure 4, are available for:
· virus concentration time history in each space;
· virus air to surface deposition time history in each space;
· individual infection risk in each space histogram;
· average number of potentially infected people in each room histogram.
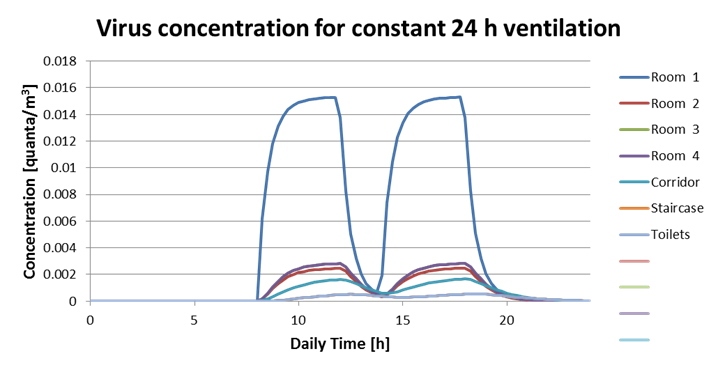
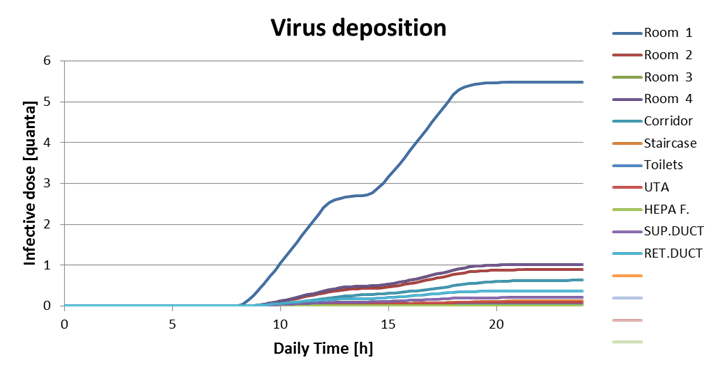
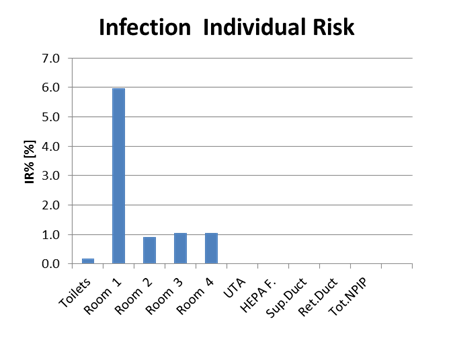
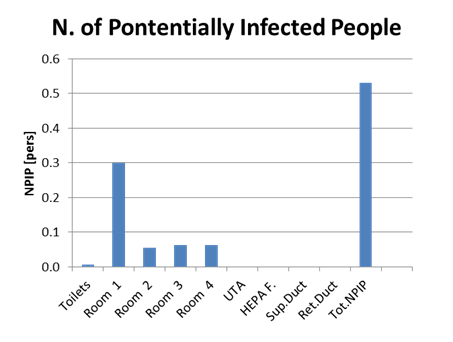
Figure 4. Tool graphic output.
The developed tool, with some limitations, allows comparing possible improvements on both ventilation solutions for new buildings/systems and retrofit and operational strategies for existing buildings/systems under pandemic condition. It is using today the infection risk probability function from Wells-Riley model to assess the infection risk, but is physically based (i.e. mass balance based) and can easily updated with different infection risk probability functions or just using virus particles concentration instead of quanta to give a RELATIVE picture of different proposed actions.
The current tool, developed under Excel using VBA programming language, is enough simple to use and fast to execute for a COMPARATIVE COVID-19 infection risk analysis for a standard building floor and the most common air distribution layout, which makes it not the most flexible tool useful for any kind of application.
This tool is intended to be used by expert only, who know the meaning of each input and their implication on the results, for the large uncertainties on several of its parameters.
Some very sensible and specific COVID-19 input parameters are provided in drop-down lists, as virus emission rate per person, susceptible people breathing rates, etc., the selection of which is under the responsibility of the tool user nevertheless they are taken from the most updated scientific sources (as reported in the disclaimer).
This tool has been produced with the intention to give to any socially responsible HVAC engineer a simple and fast to use engineering “weapon” in fighting against COVID-19 pandemic. For this reason, this tool will be freely available after the COVID-19 REHVA Task Force has evaluated its consistency and decided how practically to make it available. Look constantly at REHVA website to get informed on its release.
This work has been carried out during my mandate as AiCARR expert in the COVID-19 REHVA Task Force, the work of which was stimulus for developing the model. For this reason, I would like to acknowledge all Task Force participants and AiCARR for this opportunity.
[1] REHVA COVID-19 Task Force, 2020, REHVA COVID-19 guidance document, August 3, 2020, Brussels, https://www.rehva.eu/activities/covid-19-guidance/rehva-covid-19-guidance.
[2] Riley et al., 1978, Airborne spread of measles in a suburban elementary school, Am. J. Epidemiol. (1978), pp. 431-432.
[3] Buonanno G., Stabile L., Morawska L., 2020, Estimation of airborne viral emission, quanta emission rate of SARS-CoV-2 for infection risk assessment, Environment International, 141, https://doi.org/10.1016/j.envint.2020.105794.
Follow us on social media accounts to stay up to date with REHVA actualities
0