Stay Informed
Follow us on social media accounts to stay up to date with REHVA actualities
|
|
|
|
Marcel Loomans | Atze Boerstra | Francesco Franchimon | Chris Wisse |
Eindhoven University of Technology, Group Building Performance – Focus area IEQ and Health, EindhovenM.G.L.C.Loomans@tue.nl | bba binnenmilieu, | Franchimon ICM, | DWA |

In the light of the COVID-19 pandemic, there is a natural need to know more about the SARS-CoV-2 virus and how it develops. Ideally, we would like to look into the future and anticipate on that basis in order to limit the consequences. Building performance simulation models have been used for decades to calculate the energy demand of a building design. This may also allow us to say something about thermal comfort, for example in the event of overheating. We also use Computational Fluid Dynamics (CFD) technology to analyse the air flow in rooms and around buildings, for example ventilation efficiency. However, when it comes to ventilation and health, so far we find much less information on the prediction options. Ventilation, the flow rate/air exchange rate normally are boundary conditions and not part of the analysis of a design solution, unless it concerns fully naturally ventilated buildings. In practice, however, these are rarely designed and built. But when it comes to infections where airborne transmission is important, ventilation is crucial and depends, for example, on the use of a room and the risk that one wishes to accept. In that case, building code requirements or requirements as set out in prepared program of requirements for specific type of buildings, e.g. through labelling schemes, may not necessarily be sufficient. How do we deal with this? In this article we want to give a brief description of the model that may be used in that case, the Wells-Riley model.
The process of transmission of infectious microbiological contamination (e.g. viruses, bacteria, fungi) is not straightforward. This includes the characteristics of the pathogen, how many particles are produced in a host that is potentially pathogenic, how well the pathogen survives or remains viable outside that host (human, animal) and how good the immune system of the person who 'receives' the pathogen is. Linked to this is also the amount of viruses, bacteria or fungal spores (dose) needed to actually become ill and how this dose is received (peak or over a longer period of time). Different pathogens behave differently. For some of them the necessary information is already known, for many others, including the SARS-CoV-2 virus, this is clearly not yet the case. Fortunately, more and more knowledge is becoming available, for example with regard to the chance of survival outside the host [1,2].
In terms of transmission routes, three main routes are assumed in the transmission of pathogens that can cause respiratory tract infections such as COVID-19: the direct route via droplets, the indirect route via contact surfaces and the airborne route via aerosols. The latter route also includes faecal-oral transmission. The distinction between droplets and aerosols is normally made at the level of the size of the particle containing the pathogen. This is based on the assumption that droplets fall out quickly (deposition) and aerosols remain in the air longer. A (rather arbitrary historical) cut-off measure for this is 5 microns. Although there is consensus from aerosol scientists about the size, it should be noted that particles larger than 5 microns (even up to ~50 microns) can stay airborne for a prolonged amount of time in the indoor environment [3]. The size also determines how far a particle can penetrate the human airway system. This is another parameter with respect to sensitivity. The place where a pathogen enters the body to cause the infection, the receptor, is different for different infectious diseases and can be present at several places, more in the upper respiratory tract and/or the lower respiratory tract.
The direct and contact routes are important to recognize in the transmission of COVID-19, but for the indoor environment the airborne transmission route is something that can be influenced by the air handling systems present in buildings. Ventilation and the air flow in a room can prevent pathogens from infecting someone or limit the risk of doing so. We would therefore like to have models for this in order to be able to say something about how a certain air handling solution contributes to reducing the risk of infection.
|
Here Nc [-] stands for the number of newly infected cases over exposure time t [h], S [-] the number of people that potentially can be infected in the room to be examined, I [-] the number of infected people in the room, q [quanta/h] the amount of so-called 'quanta' produced in the room by an infected person, p [m³/h] the breathing volume flow rate of a person that potentially can be infected and Q [m³/h] the ventilation flow rate in the room to be examined. The term between brackets indicates the risk of infection in a room. It assumes a constant concentration of quanta in the room due to the production of pathogens (source) and ventilation (sink). The exponent indicates the number of inhaled quanta.
In the Equation (1), the term 'quanta' is notable. This is not a common term but has been developed specifically for this equation. Wells assumed that not every droplet/aerosol that is inhaled will lead to an infection. He then defined a quantum as the number of infected droplets (nuclei) needed to infect 1-1/e of the susceptible population in a room [4], i.e. a 63% chance of becoming infected. This number depends on, for example, the type of virus. In practice, determining the number of quanta for a particular pathogen is not straightforward. In principle, this is done by assuming available information/data and then calculating what the number of quanta has been in an outbreak at a location (e.g. a church or restaurant). With that new cases for a virus outbreak can be assessed.
The use of the Wells-Riley equation is based on a number of assumptions. These are summarized by [4,5] and relate to, among other things: - the incubation time (time between infection and the first symptoms; this means that a person infected in the situation under investigation will not contribute to the infection risk for that situation; COVID-19 is somewhat more special in the sense that the incubation time is about 5-6 days, but that infectivity can already occur 1-3 days before symptoms present themselves [6]), - the fact that a (perfectly) mixed situation is assumed with respect to the concentration of germs in the room, - that the average concentration that is inhaled during the stay is taken into account, - that the course of the infection is not taken into account, i. e. a peak, or over a prolonged period with fluctuations in concentration. In [7], as an alternative to the average concentration, the average concentration is derived from a ‘clean’ situation without pathogens present. This is closer to a practical situation in which an infected person enters a room and is present for a period of time.
The Wells-Riley model is often used when estimating the risk of infection in buildings. In the model, as shown in Equation (1), only ventilation (Q [m³/h] = lven·V; where lven [h-1] is the ventilation rate and V [m³] is the volume) is given as an option to reduce the risk using building control measures. However, more so-called 'sink' terms (l) can be added, such as inactivation of the virus (linact), deposition (ldep) and filtration (lfil) or the application of UVGI. These, in combination with the volume of the room and similar to the ventilation flow rate, can be expressed as a first order loss. For the SARS-CoV-2 virus, for example, a value of 0 to 0.63 h-1 can be used for inactivation, or 0.3 – 1.5 h-1 for deposition [7].
Examples - Application of Wells-Riley provides insight into the risk of infection. It is generally assumed that there is one infected person in the room. For the situation of the choir in Skagit Valley (USA) the risk of infection was calculated to be more than 80%. However, the parameters are sensitive to uncertainties. In particular, the production of quanta is an important parameter that can only be derived indirectly from the information available for cases.
Table 1 presents some examples of the risk of infection in different situations. The first example concerns the case of the choir in Skagit Valley in the United States. This is a well-known example, in which a large part of the people present was infected [7]. The other two examples concern an aircraft cabin and an office situation. For the aircraft situation it is assumed that the recirculation part is 100% filtered by means of a HEPA filter. This assumes that the recirculated air is free of virus particles. For the aircraft and office situation, for comparison, the effect of the use of masks is also taken into account.
Table 1. Examples of Wells-Riley application for different situations. Values used for production of quanta and respiration rate from [7,8].
Room |
| Koor Skagit Valley | Aircraft cabinet | Office room |
Volume | m³ | 810 | 480 | 240 |
Exposure time | h | 2.5 | 2.5 | 8 |
Number of infected persons | − | 1 | 1 | 1 |
Number of susceptible persons | − | 60 | 299 | 19 |
Breathing flow rate | m³/h | 1.1 (1.0) | 0.5 | 0.5 |
Production quanta | quanta/h | 970 (450) | 10 | 10 |
Mask efficiency* | − | 0 | 0 (0.5) | 0 (0.5) |
Air exchange rate | h-1 | 0.7 | 20** | 2 |
Other ‘sinks’ | h-1 | 0.62 | − | − |
|
|
|
|
|
Infection risk | % | 83 (53) | 0.1 (0.03) | 7.5 (1.9) |
Number of persons | − | 49.7 (31.5) | 0.4 (0.1) | 1.4 (0.4) |
* Applies to both infected and susceptible persons. ** including recirculated and filtered air | ||||
The results show that the chance of infection for the choir was indeed very high. Note, however, that the production of the number of quanta was derived from the available data of this case. This was determined by [7] at 970 quanta/h. Nevertheless, final values for the quanta production are still under discussion. At the moment slightly lower values are assumed [8]: 450 quanta/h for singing, 70 quanta/h for quiet talking and 5 quanta/h for breathing only. Assuming 450 quanta/h and also a slightly lower value for the breathing flow rate (1 m³/h) for the Skagit Valley case, this significantly reduces the risk to 53%. In the example we assume singing during the whole period. In practice, this will not be the case and you could be averaging over a period of time, as assumed for the aircraft and office situation (10% talking, 90% quiet; upwards rounded value). For the example of the aircraft, full (ideal) mixing is assumed. In practice, there is a form of compartmentalization of the ventilation. If we assume ten compartments, then the risk in the compartment where an infected person is sitting increases by a factor of 10.
To get an impression of the sensitivity of some parameters we refer to Figure 1 in which the effect of the quanta production, exposure time and the sum of the 'sink' terms (including the ventilation rate) on the risk of infection is visualized. Among other things, it is clear that exposure time is an important parameter in the risk of infection. For a long residence time, for example, a high ventilation rate is necessary to minimize the risk.
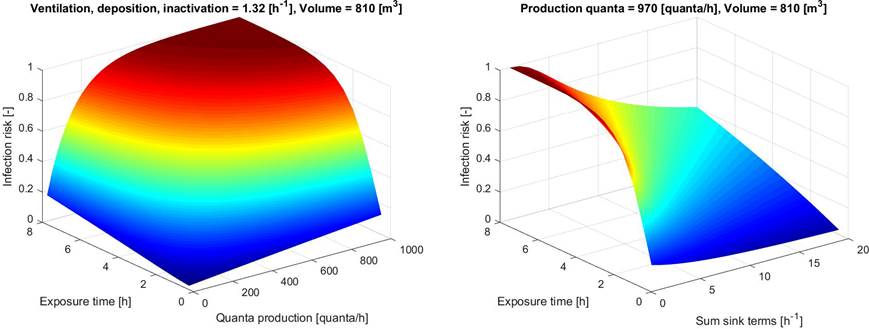
Figure 1. Sensitivity to infection risk as a function of quanta production and exposure time [left] and the sum of sink terms (especially ventilation rate) and exposure time [right]; model [7].
Restrictions - Using the Wells-Riley equation is a good way to get a better understanding of the risk of infection in a given situation and how sensitive a building or system related measure is for reducing the risk. However, there are important comments to be made when using Wells-Riley. First of all, Wells-Riley only deals with the airborne transmission route (long-range [9]). This means, more or less, that only the aerosols are looked at and not the effect of larger droplets. The risk of the direct route is therefore not treated with the Wells-Riley model. This may lead to an overestimation of the quanta for a certain outbreak if other routes are not excluded. For the corona virus, the direct route is still seen as an important route. Although aerosols also play a role in this (short-range) route [3,9], the role of ventilation in this route, without specific measures, is clearly more limited. Nevertheless, the Wells-Riley model can at least analyse and minimize the risk via airborne transmission. In addition, the assumption of perfect mixing is an important starting point. For (relatively) small rooms, or rooms with a limited height and reasonable ventilation (ventilation rate at least 1 h-1 order of magnitude), this premise will be a reasonably good approximation. For larger spaces such as monumental churches this is not necessarily the case. Here, a trade-off will have to be made, for example, by including part of the volume in the analysis or by assuming a certain ventilation effectiveness.
Alternatives – In order to be able to say something about the spread of virus particles in a room, the airflow in the room will have to be modelled. This can be done using Computational Fluid Dynamics (CFD). Although this technique provides insight into how particles move in a room, and in theory the exposure to quanta could be determined, it is much more complex than the Wells-Riley model. The latter therefore is preferred for determining the risk of infection. However, in order to investigate the effect of a ventilation solution and variants thereof, or of a so-called cough screen, CFD could be used. For the purpose of validation, these simulations should be combined with measurements.
Because every situation is different and therefore the risk of infection, a webtool has been developed that allows to assess the risk yourself. An example of that is presented in eerstehulpbijventilatie.nl (in Dutch: ‘first aid for ventilation’). The webtool is just one example of the several tools that have been developed over the last months. The other tools generally reside as an Excel-tool, though webtools are appearing in parallel as well. Most are based on the Wells-Riley equation, several assuming the transient approach as presented by [7]. The Dutch webtool initially was developed for application in a church building, with a focus on singing during a service. Further development towards a more generic tool is planned and is expected to be online in October.
The current Dutch webtool allows to calculate the risk of infection based on the specified number of people. It also calculates the R0 value, i.e. how many people are potentially infected by one infected person in a given situation. In principle, you want to keep that value < 1. The user can compare this with the displayed infection risk/contamination risk.
This webtool is based on the model described by [7]. It assumes a starting situation where there is no contamination in the room and is a more extended version of Equation (1). It describes the build-up of the concentration over time, just like the well-known models that describe the CO₂ concentration in a room (see Figure 2 on the left). Figure 2 (right) shows the parallel build-up of the quanta concentration. The original equation (Equation (1), by definition, will show higher risks.
Figure 2. Build-up of the CO₂ concentration [left] and the comparable build-up of the quanta concentration [right]. Equation (1) uses the limit value (black dotted line - right).
In the model choices have been made for the production of quanta and for the breathing volume. As far as quanta is concerned, the following values are used: 450 q/h for singing, 10 q/h for listening during the church service. For the breathing flow rate: 1.0 m³/h is assumed for singing and 0.5 m³/h for listening. The 'sinks' are not included. For the user a 'traffic light' has also been added, to indicate the risk of infection. Up to and including 1%: green; from 1% up to and including 5%: orange; above 5%: red. This is of course a choice and does not mean that if the risk is less than 1% no one can get sick. The webtool also calculates the maximum number of people that may be present so that a maximum CO₂-concentration of 800 ppm is not exceeded (‘class A'). Also, with this number of persons an R0 value is provided. In this way the user can compare the outcome to the number of people that originally was entered. The maximum number of people that can use a room is related to the 1.5 m distance protocol. Finally, to repeat, knowledge about the virus is still developing. This concern, for example, the amount of quanta and the contribution of the airborne transmission route to the infection risk. The information presented here should be seen in that light, and as a supplement to the current measures to reduce the risk of infection.
The modelling of the airborne infection risk has a sudden renewed focus. Until now, outside the care and cure environment, this risk has not yet been included (consciously) a lot in the design of buildings and its air handling systems. Current experiences once again remind us that air quality and ventilation is more than perception and a not too high CO₂ level as a proxy for the concentration of all other, in general, chemical substances that may be present in the air. Recognizing the biological component offers the opportunity to put ventilation in buildings in a broader perspective. The use of the Wells-Riley model makes it possible to do so in a more quantified way. Despite the limitations of the model, at least the effect of variants can be compared. With that, the application of other techniques for reducing the risk also gets a better comparison.
This article is a (nearly) directly translated version of the article that was prepared for TVVL Magazine (Nr.5 – October). For the initial translation DeepL has been applied.
[1] N. Van Doremalen, T. Bushmaker, D.H. Morris, M.G. Holbrook, A. Gamble, B.N. Williamson, A. Tamin, J.L. Harcourt, N.J. Thornburg, S.I. Gerber, J.O. Lloyd-Smith, E. De Wit, V.J. Munster, Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV-1, N. Engl. J. Med. 382 (2020) 1564–1567. https://doi.org/10.1056/NEJMc2004973.
[2] J.A. Lednicky, M. Lauzardo, Z. Hugh Fan, A. Jutla, T.B. Tilly, M. Gangwar, M. Usmani, S.N. Shankar, K. Mohamed, A. Eiguren-Fernandez, C.J. Stephenson, M.M. Alam, M.A. Elbadry, J.C. Loeb, K. Subramaniam, T.B. Waltzek, K. Cherabuddi, J. Glenn Morris, C.-Y. Wu, Viable SARS-CoV-2 in the air of a hospital room with COVID-19 patients, Int. J. Infect. Dis. 0 (2020). https://doi.org/10.1016/j.ijid.2020.09.025.
[3] W. Chen, N. Zhang, J. Wei, H.L. Yen, Y. Li, Short-range airborne route dominates exposure of respiratory infection during close contact, Build. Environ. 176 (2020) 106859. https://doi.org/10.1016/j.buildenv.2020.106859.
[4] C.J. Noakes, P.A. Sleigh, Mathematical models for assessing the role of airflow on the risk of airborne infection in hospital wards, J. R. Soc. Interface. 6 (2009). https://doi.org/10.1098/rsif.2009.0305.focus.
[5] S.N. Rudnick, D.K. Milton, Risk of indoor airborne infection transmission estimated from carbon dioxide concentration, Indoor Air. 13 (2003) 237–245. https://doi.org/10.1034/j.1600-0668.2003.00189.x.
[6] World Health Organization, Coronavirus disease 2019 (COVID-19) - Situation Report-73 HIGHLIGHTS, (2020) 13. https://doi.org/10.3201/eid2606.200239.
[7] S.L. Miller, W.W. Nazaroff, J.L. Jimenez, A. Boerstra, G. Buonanno, S.J. Dancer, J. Kurnitski, L.C. Marr, L. Morawska, C. Noakes, Transmission of SARS-CoV-2 by inhalation of respiratory aerosol in the Skagit Valley Chorale superspreading event, MedRxiv (Accepted Indoor Air). (2020) 2020.06.15.20132027. https://doi.org/10.1101/2020.06.15.20132027.
[8] G. Buonanno, L. Morawska, L. Stabile, Quantitative assessment of the risk of airborne transmission of SARS-CoV-2 infection: prospective and retrospective applications, Environ. Int. (2020) 106112. https://doi.org/10.1016/j.envint.2020.106112.
[9] L. Liu, Y. Li, P. V. Nielsen, J. Wei, R.L. Jensen, Short-range airborne transmission of expiratory droplets between two people, Indoor Air. 27 (2017) 452–462. https://doi.org/10.1111/ina.12314.
Follow us on social media accounts to stay up to date with REHVA actualities
0