Radiant ceilings combined with diffuse ventilation – a numerical parametric study of cooling performance

Abstract

Focus on indoor comfort, energy savings and Near-Zero Energy Buildings (NZEB), and the focus on finding new approaches for heating, cooling and ventilation increases. Suspended radiant ceiling panels combined with diffuse ventilation offers a novel approach for integrating heating, cooling, ventilation and acoustics for high-performing NZEB buildings. This paper presents a numerical parametric study of a perforated suspended ceiling with embedded hydronic pipes where the ceiling perforations are used for diffuse ventilation. The investigations focus on the heat transfer coefficient from the ceiling to the room and from the ceiling to the plenum in cooling mode. A suspended gypsum ceiling with embedded pipes was investigated with and without ventilation.  The investigations were carried out in the multi-physics simulation program COMSOL with different scenarios of pipe spacing, materials, dimensions, and surface heat transfer coefficients. The objective of the investigations was to identify several solutions for a ceiling panelthat promises to combine heating, cooling, ventilation and acoustic performance for future NZEB buildings – in short HCVA ceiling panels. The investigations indicate a potential heat transfer increase from an HCVA panel of 30–45% compared to a stand-alone radiant ceiling. The increase is mainly due to the increased convective heat transfer in the plenum which cools the ventilation supply air before it enters the occupied zone.

1 Introduction

The international strive to achieve a comfortable indoor environment and increase productivity of building occupants while saving energy has led to increasing demands on novel approaches to heating, cooling and ventilation of buildings. One such novel approach is to combine hydronic radiant ceilings with diffuse ceiling ventilation.

Diffuse ceiling ventilation is characterized by using a large perforated surface to supply air to the room. This ventilation concept uses the void between the floor slab and the suspended acoustic ceiling, the so-called plenum, to create a positive pressure chamber that forces the air through the acoustic perforations and into the room. It allows for air to enter the room at significantly reduced inlet velocity, which seems to impact draught and noise positively [1]. It also simplifies the building process because air terminals and some of the ductwork installation can be omitted [2].

There are several types of hydronic radiant ceiling systems and they can be separated into three categories [3]:

1.    Pipes embedded deep in the main structure (Thermally Active Building Systems, TABS)

2.    Pipes isolated from the main structure (radiant surface systems)

3.    Radiant heating and cooling panels (pipes suspended from the floor separation slab).

In this paper, the focus will be on the 3rd option –suspended radiant ceiling system with pipes embedded in the perforated acoustical ceiling panel and suspended from the slab. The radiant ceiling provides a large heat transferring surface in the room that allows heating and cooling to be supplied at temperatures that are close to the room comfort temperature.

The hydronic radiant ceiling in combination with diffuse ventilation is a promising option for merging heating, cooling, ventilation and acoustics services in one building component. Previous similar studies have mainly been on combinations with TABS system. One approach of combining TABS with diffuse ventilation was performed by Yu et al. and Zhang et al. [4], [5], but the heat transfer to the room is reduced significantly due to the acoustical perforated ceiling panels covering the TABS slab completely.

This has led to the investigation of embedding the pipes in the suspended ceiling, and to start quantifying the thermal performance: can the radiant ceiling provide heating and cooling for the plenum for pre-cooling/heating the ventilation air and for the room below to ensure indoor comfort. Experimental studies by Eriksen & Christiansen [7] and Onsberg & Eriksen [8] showed higher heat transfer from the radiant ceiling when combined with diffuse ventilation and Krusaa et al. [6] employed the principle in a simulation study that proved adequate indoor comfort and significant energy savings for different room types. However, more thorough investigation of the heat transfers from the ceiling need to be made to confirm the hypothesized superior thermal performance.

The objective of the present study was to numerically study a combined ceiling panel for heating, cooling, ventilation and acoustics – the HCVA panel – to disclose the expected cooling performance increase when the suspended radiant ceiling also acts as the air terminal device. The investigation is carried out as a parametric numerical study to help identify the most sensible parameters and understand their effect.

2 Methods

The thermal performance of the HCVA panel was simulated in the multi-physics numerical tool COMSOL version 5.3, using the 2D model environment with the physics for “Steady-state Heat Transfer in Solids”.

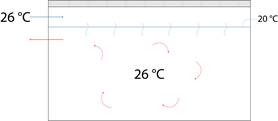
Figure 1. Reference room with the HCVA panel in a cooling scenario.

The radiant acoustical ceiling was a sandwich construction consisting of an aluminium heat distribution plate placed between two perforated gypsum tiles (600 x 600 mm), see Figure 2 and Figure 3.

Figure 2. The reference radiant acoustical ceiling panel, depicted with slightly too large pipes.

2.1 Reference model

The reference model forms the basis from where the different scenarios have been tested. A cross-section of the reference model is depicted in Figure 3.

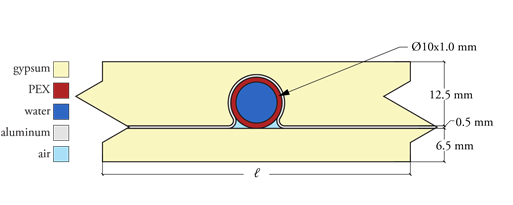
Figure 3. Cross-section of reference model.

The reference model had a c-c distance between the pipes (from centre to centre) of 300 mm. The material properties are listed in Table 1.

Table 1. Material properties.

For the reference model without ventilation, the surface heat transfer coefficients from the ceiling to the plenum (hs,p) and from the ceiling to the room (hs,r) were calculated using the ASHRAE handbook [9] to be 6 W/m²K and 10 W/m²K [10], respectively, including both radiative and convective heat transfer. For all parametric studies, the air temperature was kept the same in both plenum (Tp) and room (Tr) at 26°C and a temperature of 22°C as a boundary for the water (Tw), i.e. cooling mode.

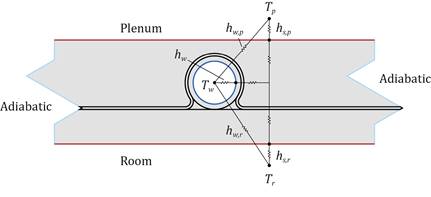
Figure 4. Boundary heat transfer and temperatures used for the calculations.

2.1.1 Preliminary research for heat transfer coefficient in plenum

Building simulation tools often uses fixed heat transfer coefficients for the enclosure surfaces, often ignoring airflow rate and inlet type. With the combined panel proposed in this paper, the upward surface heat transfer coefficient is of crucial importance to the total heat transfer. And the heat transfer coefficient varies with airflow rate and inlet type in the plenum as well as the temperature difference between supply air and mean plenum temperature.

Consequently, preliminary studies of the convective heat transfer coefficient was made in CFD by Eriksen & Christiansen [7] for heating and cooling scenarios. In order to qualify the results, we plotted them in relation to Spitler [11] and Fisher [12], who made studies of the convective heat transfer coefficients in an enclosure for different air change rates. Spitler and Fisher found that the relation was predominantly determined by the jet momentum J:

Where

      =air flow [m³/s]

        =velocity of supply air [m/s]

        =9.82 [m/s²]

 =volume of room (plenum) [m³]

In Figure 5 the results are plotted for the resulting jet momentum. Spitler found that the jet momentum correlation was valid for Ar < 0.3 which is the case for all parametric scenarios in this paper.

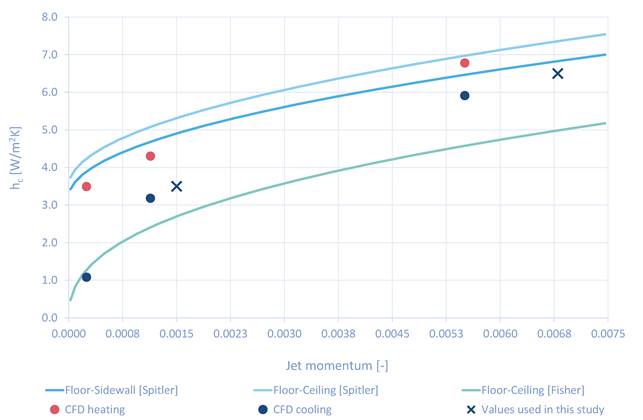
Figure 5. Heat transfer coefficient on floor for different inlet surfaces (sidewall jet and ceiling diffuser). Adapted from Fisher and Spitler (solid lines). CFD results for heated and cooled floor as dots (Eriksen and Christiansen, [7]).

The results in Figure 5 from Eriksen & Christiansen show that as buoyant flows become more predominant (low jet momentum) the convective heat transfer reduces. This effect is more pronounced for cooled floors due to stratification. Considering the advances in CFD, we use the calculated upward surface heat transfer coefficient hs,p from Eriksen & Christiansen. The values are shown in Table 2.

Table 2. Upward surface heat transfer coefficient hs,p. Low and high diffuse ventilation rate correspond approx. to the hourly airchange in open plan office and meeting room.

2.2 Parametric study

Table 3 lists the parametric investigations of the combined ceiling panel: the pipe distance, the aluminium thickness, insulation on top of the ceiling, and different surface heat transfer coefficients.

Table 3. Scenarios in project. Reference case in bold.

The pipe distance was tested for a c-c of 100, 150 and 300 mm to have as few pipes in the ceiling as possible for maintenance and costs reasons, but still have sufficient capacity for a low-energy building.

The aluminium thickness of the heat distribution plate was changed to 0.7 mm and 1.0 mm, to quantify the impact of a thicker heat conducting layer.

The surface heat transfer coefficient was changed on top of the plate to mimic the effect of diffuse ceiling ventilation. The value was changed from 6 W/m²K (stagnant air, no diffuse ventilation) to 9 W/m²K and 12 W/m²K which corresponds to approximate ventilation rates of an open plan office and a meeting room.

The influence of the insulation on top of the ceiling was tested because it is important to the acoustic properties of the ceiling panel. In the investigation 40 mm insulation (45 mW/m²K) was placed on the top. The insulation thermal resistance and the upward surface resistance were lumped into one heat transfer coefficient of 1 W/m²K.

Also, the effect of the gypsum core conductivity was tested, to quantify the impact of using a thermally high-conducting gypsum board with a blend of graphite (0.52 W/mK).

2.2.1 Impact of acoustical perforations.

The acoustical perforations of the ceiling panel are essential for both the acoustics and for the ventilation air to pass through. A standard heat distribution plate has no holes to let the air and sound pass through. Therefore, the heat distribution plate must be perforated in order to ensure the acoustical performance. However, the perforations have a negative impact on the heat transfer of the plate. Consequently 5 different patterns were also tested, Figure 6.

Figure 6. Illustration of the perforations in the combined gypsum and aluminium plates.

3 Results and analysis

The results show the impact of different design decisions on the thermal performance of radiant ceiling panels combined with diffuse ventilation.

3.1 Impact of acoustical perforations

The results for the acoustical perforation showed that the heat flux for the “Line” perforations are reduced with 7.4%, where the “Hex” showed a reduction of between 5.6-13.1% compared to the Basic plate without any perforations. A preliminary 3D-model of line-plate showed only a reduction of 3-4%. This means that the 2D heat transfer results presented below should be conservatively reduced by the same magnitude.

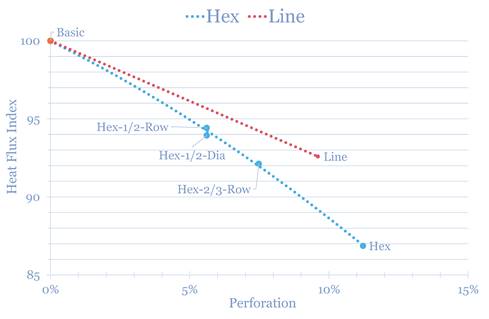
Figure 7. Heat flux of plate vs. perforation percentage.

3.2 Parametric study

Figure 8 show the temperature field of the reference model with different pipe spacing and a comparison with and without the aluminium plate. As it can be seen the effect of adding a heat distribution plate is quite significant on the temperature field.

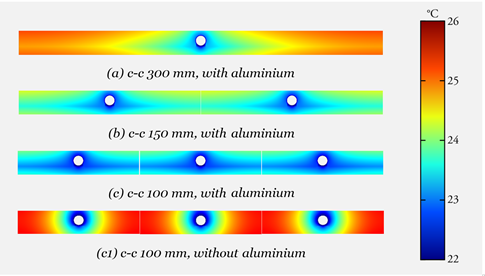
Figure 8. Temperature gradient of the reference model (a) with c-c 300 mm, (b) cc 150 mm, (c) cc 100 mm and (c1) cc 100 mm without an aluminium plate.

The surface temperatures for the reference model with aluminium can be found in Figure 9. Smaller distance between the pipes gives a more even temperature distribution on both upward and downward ceiling panel surfaces.

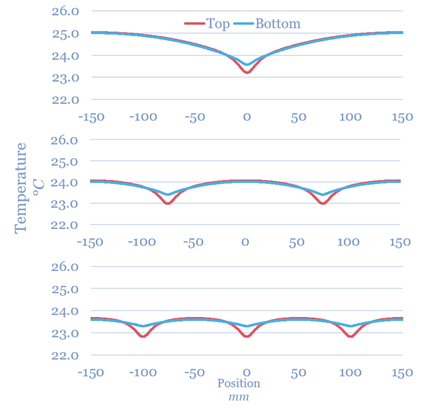
Figure 9. Surface temperatures for Reference model c-c 300, c-c 150 and c-c 100 mm with a water temperature of 22°C, and plenum and room air temperature of 26°C.

Figure 10 shows only a very small performance increase of using thicker aluminium. The impact is almost independent of pipe c-c distance.

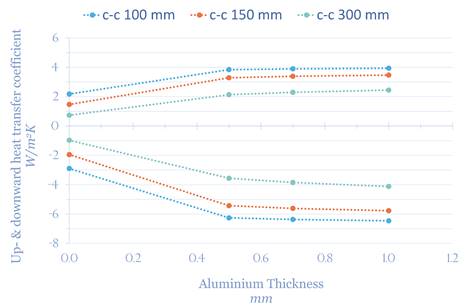
Figure 10. Up- and downward heat transfer coefficient with different heat distribution plate thicknesses.

The upward and downward heat transfer in relation to the upward surface heat transfer coefficient, i.e. the rate of diffuse ventilation, is shown in Figure 11. As expected, the effect on the top of the ceiling panel, hence the heat transfer from the ceiling panel to the plenum, is most significantly affected. The heat transfer to the room below is only changed by a small fraction.

When the reference gypsum board material is changed to a high-conducting gypsum-graphite blend, the heat transfer increases approx. 7%. Without the aluminium the effect of graphite board is larger (30–45%). However, looking at the heat transfer without aluminium but with graphite for the pipe spacing of 100 mm, and comparing with the pipe spacing of 300 mm with aluminium there is a small increase of 13% from the pipe spacing of 300 to 100 mm.

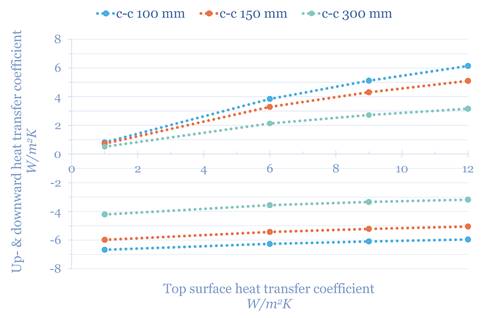
Figure 11. Up- and downward heat transfer coefficient with different top surface heat transfer coefficient.

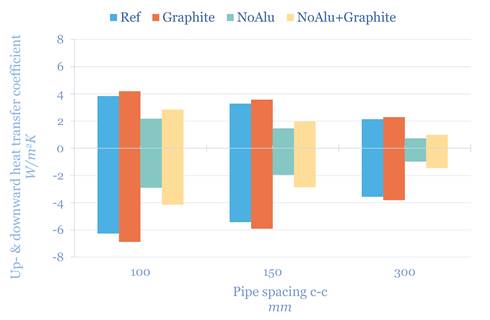
Figure 12. The effect of using a gypsum board material with higher thermal conductivity with and without aluminium plate.

The heat transferred from the ceiling to the plenum re-enters the occupied zone, when the plenum air passes through the ceiling panel. The heat fluxes between HCVA panel, slab, occupied room and ventilation during operation of the systems are complex to deduct analytically and requires a full building simulation model to be investigated in detail.

The plenum walls and slab are essentially adiabatic except the façade wall, but to be conservative we assume that only 50% of the cooling initially ‘lost’ to the plenum is regained by the diffuse ventilation concept. This means the room is cooled by direct heat transfer from the ceiling panel and indirect heat transfer by the ventilation supply air due to pre-cooling in the plenum. In Figure 13 scenarios with different surface heat transfer coefficients (hs,p) are compared to the reference model with index 100. The direct and indirect heat fluxes are lumped together assuming 50% of the indirect heat is regained. For the pipe spacing c-c 300 mm, the insulation on top of the ceiling (hs,p = 1 W/m²K) causes an increase on the total heat transfer from the ceiling of approx. 25%. In comparison the increase caused by adding diffuse ventilation (9 & 12 W/m²K) is 30%, but only with a small difference between high and low ventilation rates. For 100 mm c-c spacing, the total heat transfer is increased up to 45%.

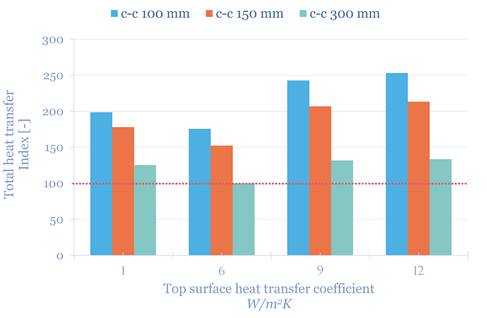
Figure 13. Total heat transfer index for the different top surface heat transfer coefficients. Index 100 is the reference model with c-c 300 mm with hs,p = 6 W/m²K.

4 Discussion

4.1 Impact of acoustical perforations

The perforations influence the total heat transfer. The investigations illustrated in this paper showed that the perforations are important to remember. However, the studies were made in 2D and preliminary studies showed the impact of the perforations is larger in 2D than in 3D. Consequently, further investigations should be carried out with 3D simulations to determine the exact decrease in the heat flux due to the perforations.

4.2 Parametric study

Adding the aluminium plate to the ceiling panel has a significant effect on the temperature field in that the cc300 mm with aluminium outperforms the cc100 mm without aluminium. The thickness of the aluminium plate does not have a significant impact. Adding graphite to the gypsum core has only a small impact when a heat conducting plate is implemented, however, for ceiling panels that rely only on small c-c spacing, the graphite increases the heat flux noticeably.

The downward heat transfer is almost not affected by the top surface heat transfer coefficient which is surprising as we expected insulation placed on top of the ceiling to be a performance increasing measure.

The assumption that energy initially ‘lost’ to the plenum is regained because of the diffuse ventilation concept is uncertain. It is influenced by the radiative and convective heat flux ratio in the plenum and the thermal storage capacity of the materials in the plenum and the daily temperature shift as well. The regain percentage will need further investigations in dynamic situations to disclose the true extra cooling capacity of the HCVA ceiling.

5 Conclusion

The overall objective was to quantify the effect of combining radiant ceiling panels with diffuse ventilation. We hypothesized correctly that the interaction between the ventilation air and the ceiling panel would cause the total heat transfer from water to room air to increase. In the process we studied the impact of a heat distribution plate, the spacing between pipes, gypsum material properties and the effect of the surface heat transfer coefficient in order to identify a number of solutions for an HCVA ceiling panel that combines heating, cooling, ventilation and acoustics with the best possible thermal performance.

Looking at the impact of adding the diffuse ventilation the heat transfer increases 30-45%. The difference between low and high diffuse ventilation rate was only 5%.

As a closing remark, we would like to acknowledge Saint-Gobain Nordic and Innovation Fund Denmark for financial support of this work.

References

[1]    J. Fan, C.A. Hviid, H. Yang, Energy Build.59, 73-81 (2013)

[2]    C.A. Hviid, S. Svendsen, Energy Build. 56, pp. 160-168, 2013.

[3]    F. Causone, S.P. Corgnati, M. Filippi, B.W. Olesen, Energy Build.41, no. 6, 622-628 (2009)

[4]    T. Yu, P. Heiselberg, B. Lei, M. Pomianowski, C. Zhang, R. Jensen, Energy Build.105, 165-177 (2015)

[5]    C. Zhang, T. Yu, P. Heiselberg, M. Pominaowski, P. Nielsen, DCE Technical Rep. no. 27 (2016)

[6]    M.R. Krusaa, C.A. Hviid, and J. Kolarik, AIVC (Nottingham, U.K., 2017)

[7]    F.V. Eriksen, N.B. Christiansen, DTU Byg, M.Sc. thesis (2017)

[8]    R. Onsberg, M.S. Eriksen, DTU Byg, M.Sc. thesis (2014)

[9]    HVAC systems and equipment, ASHRAE Handbook. American Society of Heating, Refrigerating and Air-Conditioning Engineers (Atlanta, 2012)

[10]  DS 418, Calculation of heat loss from buildings, Dansk Standard (2011).

[11]  J. Spitler, P. Pedersen, D. Fisher, ASHRAE Transactions97 505-515 (1991).

[12]  D.E. Fisher, C.O. Pedersen, ASHRAE Transactions103, 2 (1997)