Stay Informed
Follow us on social media accounts to stay up to date with REHVA actualities
|
|
|
|
Dirk Müller | Kai Rewitz | Dennis Derwein | Tobias Maria Burgholz |
Institute for Energy Efficient Buildings and Indoor Climate (EBC), RWTH Aachen University and Heinz Trox Wissenschafts gGmbH, Aachen | Institute for Energy Efficient Buildings and Indoor Climate (EBC), RWTH Aachen University. | Institute for Energy Efficient Buildings and Indoor Climate (EBC), RWTH Aachen University. | Heinz Trox Wissenschafts gGmbH, Aachen |
The continuing risk of infection with COVID-19 (Coronavirus SARS-CoV-2) has led to intensive discussions in many countries about how different rooms can be used in the future. It should be noted that there will always be a risk of infection in rooms with several people, as transmission of the virus cannot be ruled out without the use of an unreasonable amount of protective clothing that goes beyond mouth-nose protection in everyday life. Viruses can be transmitted between people via three different ways without direct physical contact:
· Contact surfaces
· Droplets
· Aerosols
The transmission of viruses via contact surfaces can be significantly reduced by regularly cleaning all relevant surfaces and disinfecting the hands. Transmission by droplets is also significantly reduced by wearing a mouth-nose protector. Neither transmission path is directly influenced by the use of ventilation systems. At temperatures below typical room temperatures, viruses may remain active on surfaces for a longer period of time (Chan et al. 2011) which is not taken into the following considerations, just like the influence of relative humidity.
The present contribution focuses on the transmission of viruses by aerosols, since this transmission path cannot be prevented by simple measures and is responsible for the critical spread of viruses in closed rooms. Aerosols are very small particles, which can be produced by human respiration, for example. Ventilation of the room can directly influence the concentration of aerosols contaminated with viruses. Therefore, this transmission path is of particular importance for safety assessments of rooms and events in ventilated rooms.
A simplified analysis of the complex transportation processes by aerosols in ventilated rooms is described, which allows an estimation of the risk of infection in different rooms and usage situations. This analysis explicitly does not deal with medical or individual-related factors, since the focus is on the technically adjustable parameters of different rooms or ventilation systems. With the introduced calculation model, it can be estimated, which risk of infection exists, standardized to a reference state, and in which rooms special precautions for infection protection should be taken.
Based on this approach it can be shown that the air exchange rate, the room volume, the length of stay and the occupancy of the rooms significantly influence the relative risk of infection. Especially in rooms with relatively high room occupancy and long durations of stay, high air exchange rates generated by mechanical ventilation are necessary to reduce the relative risk of infection by aerosol-bound transmission of viruses.
In the transmission of respiratory diseases, the World Health Organization distinguishes significantly between the three mechanisms (World Health Organization 2014):
In direct contact transmission, a virus is transmitted through direct skin and mucous membrane contact without the virus using another medium for its transport route.
Indirect contact transmission is the transmission of a virus to one or more non-infected persons by a process known as droplet transmission. In droplet transmission, viruses are transmitted by spraying infectious droplets from the airways of an infected person onto the mucous membranes or conjunctiva of non-infected persons in the near field of the infected person.
The larger droplets relevant for droplet infection have a significant sink rate, so that they settle on the ground or other surfaces within a few seconds (Wells 1934). During this flight phase, they cover a distance of about 1.5 m.
Since the droplets settle quickly on surfaces, transmission can also occur through contact with contaminated surfaces if, after surface contact, the person subsequently transports the viruses into the area of their own conjunctiva or mucous membranes, for example, via their hands (WHO 2014).
In the case of aerosol transmission, viruses can be transmitted from an infected person to a larger number of uninfected persons by means of very small droplets or particles. Droplets below a critical particle size can evaporate during the flight phase to form so-called droplet nuclei. These droplet nuclei consist partly only of solid residues and have the potential to be transported as aerosol in the ambient air for several hours due to their low mass and the resulting low sinking speed. WHO classifies airborne particles with a particle diameter of at least 5 µm as droplets. Particles that consist only of solid residues as well as droplets below a particle diameter of 5 µm are summarized as droplet nuclei (World Health Organization 2014). In the following, airborne droplet nuclei are referred to as aerosols according to this classification.
If aerosols are formed from the sputum of people with respiratory diseases, there is a risk of infection through inhalation of these aerosols, as the small particles may be contaminated with viruses. A critical factor in this transmission path is that the usual measures such as hand hygiene, keeping minimum distances and wearing simple mouth-nose covers are only partially or almost not effective (World Health Organization 2014). The formation of droplets and aerosols is clearly shown in Figure 1.
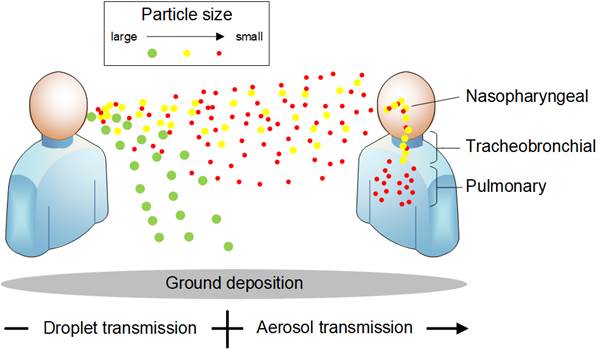
Figure 1. Schematic representation of propagation mechanisms according to (Pan et al. 2019).
In view of the current SARS-CoV-2 pandemic, the role of aerosols in the transmission of the virus is intensively discussed in science and studied worldwide.
Recent studies have shown that aerosol transmission in combination with unfavorable ventilation conditions can lead to transmission of SARS-CoV-2 (Guenther et al. 2020; Li et al. 2020). In view of the data available to date, scientists expressly warn of the danger posed by aerosol transmissions with SARS-CoV-2 (Fineberg 2020). Possible measures for the containment of aerosol transmissions indoors are ventilation measures that result in a high outdoor air exchange rate, low air circulation and a rapid removal of breathable air, in particular (Morawska and Cao 2020; Somsen et al. 2020). In order to quantify the effectiveness of these measures more precisely, the effects of ventilation or air purification on the contamination of indoor air with viruses must be investigated in more detail.
In the following, this paper will focus on the spread of viruses through aerosols. This transmission path cannot be effectively suppressed by classical measures such as regular disinfection of a surface or wearing a mouth-nose cover.
The type of airflow in a room plays a central role in the spread of viruses indoors. The majority of all mechanically ventilated rooms have mixed ventilation. With ideal mixed ventilation, all impurities and particles are distributed evenly throughout the entire room volume, so that there are no local concentration differences. The theory of ideal mixed ventilation assumes that the air movements caused by ventilation, thermal forces and diffusion are sufficient to distribute all local emissions evenly throughout the room volume.
In practice, higher concentrations of pollution can occur locally in real mixed ventilation systems.
In addition to mixed ventilation, displacement ventilation/layer flow and displacement flow are also used in practice. While displacement flows are limited to special areas such as a clean room and are therefore not considered further in the following, displacement flows are often used in particular for rooms with higher ceilings.
The propagation of pollutants in the room and the main parameters of ventilation efficiency are described in the REHVA Guidebook on Ventilation Effectiveness (Mundt 2004). The air exchange efficiency is a measure for the flushing of a room. The ventilation efficiency considers the removal of local emissions.
In this paper, all investigations will refer to the approach of an ideal mixed ventilation. An evaluation of a source air flow is planned for a later date.
It should be noted that even if a room is freely ventilated by open or tilted windows, a mixed or displacement air flow can be generated. In the case of free ventilation, however, it is difficult to give an exact value for the air exchange. The exchange of air with the environment depends on the type of window opening and frame geometry as well as wind and temperature conditions. A transfer of the results to the case of free ventilation is only possible with the restrictions mentioned above.
If there is at least one infected person in a room, viral aerosols are potentially released into the room air. In the case of ideal mixed ventilation, the polluted aerosols are distributed throughout the entire room volume and the concentration of the aerosols polluted with viruses can be calculated from the emission rate of the virus-carrying particles and the outdoor air volume flow. The room air volume only has an effect if the dispersion processes are considered transiently. In a stationary state, only the fresh air volume flow rate is decisive as a room air technical parameter.
For the evaluation of transient effects in room air flows, the nominal time constant τncan be used, which indicates the fastest possible time for an air change:
| (1) |
As trace gas investigations show, stationary states in the room air are reached after about five space-time constants.
Transmission of infection in a room via aerosols cannot be ruled out under the protective measures in use today. Although this transmission route is very complex and many medical details are only partially known, the following section will derive a model in which rooms of different sizes and uses can be compared with regard to the existing risk of infection. This simplified model is subject to restrictions, which will also be discussed in the following sections. It should be noted that the decay curves of functional SARS-CoV-2 viruses on aerosols under different room air conditions are not known. Therefore, for all subsequent calculations it is assumed that there are no significant differences between SARS-CoV-2 viruses in different indoor air conditions. This assumption may, however, be inadmissible, especially in rooms with very different relative humidity, since humidity has been shown to have an influence on the decay rate of functional viruses in aerosols (Smither et al. 2020). Since the current state of research does not allow an exact quantification of this effect, this effect is neglected in this paper.
In the literature, approaches can be found that describe the risk of infection as a function of the quantity or number of inhaled viruses. A well-known approach is the Wells-Riley model (Riley et al. 1978). This approach was originally developed to model infection chains of a measles outbreak in an elementary school. The risk of infection is determined here based on a so-called "quanta concentration" in the indoor air. A quantum describes the amount of virus that must be ingested by a person to become infected with a given probability. The risk of infection ARInf after Wells-Riley is described by equation (2).
| (2) |
Here, I corresponds to the number of infected persons in a room, q stands for the "quanta emission rate", i.e. the rate of quanta that an infected person emits into the indoor air. The pulmonary ventilation rate of a person is denoted by p, with τ indicating the time that a non-infected person stays in the aerosol-loaded environment. The air exchange rate of the room is described with the abbreviation LW. The equation is based on the assumption that the infected and infectious persons are in the room at the same time and that the "quanta concentration" in the ideally mixed room air corresponds to the equilibrium concentration for the entire period (Riley et al. 1978).
In this approach, the "quanta emission rate" is a hypothetical quantity and not a directly measurable quantity, since it can usually only be determined empirically from the reproduction number in transmission chains in epidemic studies. Reproduction rate is an epidemiological variable and describes the average number of persons infected by an infected person (Robert Koch Institute 2020a). The calculation of this quantity is therefore subject to a high degree of uncertainty, especially since in these studies the transmission mechanism cannot always be clearly attributed to aerosol transfer (Azimi and Stephens 2013). Despite this uncertainty, in the current SARS-CoV-2 pandemic, this approach has been used in several studies to assess the risk of indoor infection from aerosol transmission (Dai and Zhao 2020; Sun and Zhai 2020; Buonanno et al. 2020).
For a simplified approach to assessing the risk of infection in a room contaminated with virus-carrying aerosols, the following simplified assumption states that the risk of infection increases linearly with the number of inhaled viruses. The risk of infection in this model is thus proportional to the number of inhaled viruses. This consideration corresponds to a linearization of the Wells-Riley model, where here the virus quantity is not considered in the form of quantum, but as the number of viruses. The validity of this linearization could not be checked so far. However, the linearization is an important assumption in this paper in order to avoid quantifying the medical effects that are relevant for aerosol transmission. The use of the Wells-Riley model would not allow this circumvention. Therefore, the risk of infection ARInf can be defined according to equation (3) as the product of the number of inhaled viruses nV and an infection parameter κInf. The infection parameterκInf includes all processes that are decisive for triggering an infection, apart from the inhaled virus quantity. At this point, no medical or personal effects during the transmission process of the virus are considered for modeling purposes. Neither will it be considered what other medical circumstances must be taken into account for a person to become ill. For comparing rooms of different designs and uses, all complex factors are compared using the infection parameter κInf for an average person as given.
| (3) |
The number of inhaled viruses nV can generally be calculated from equation (4) using the temporal integral of the virus concentration ζ (t) in a room at the time t as well as the respiratory volume flow V̇A where under stationary boundary conditions during the entire duration of the stay τ a mean virus concentration ζ̅ can be accepted.
| (4) |
In this model approach, the mean virus concentration ζ̅ in a room can be determined according to equation (5) from the exhaled aerosol volume flow contaminated with viruses ṅAerosol of a person, the volume flow rate decisive for the air exchange of the room V̇R, and a probability value for the presence of at least one infected person PKRP. Concentration effects that occur when an infected person enters the room are neglected here. However, the effect of concentration has a greater influence especially in the case of short residence times compared to the respective nominal time constant. In this balance, the number of viruses inhaled by the persons in the room is also neglected.
| (5) |
The probability PKPR at ninf infected persons in a total population np meeting at least one infected person in a group with nR people in a room is approximated by equation (6) (Consileon Business Consultancy GmbH 2020; Tabarrok 2020).
| (6) |
This leads to the absolute risk of infection ARinf according to equation (7):
| (7) |
With this equation, the absolute risk of infection in any room can be calculated based on the simplifications described. However, an evaluation and interpretation of the results remains difficult, since some parameters of this equation cannot be given with sufficient certainty. Therefore, in the next section the relative risk of infection in a room is dealt with.
Under normal living conditions, it must be assumed that even if recommended precautions and rules of conduct are strictly adhered to, an infection with COVID-19 in rooms can never be completely ruled out. The absolute risk of infection is never zero if there are at least two people in a room. For a simplified risk assessment, a reference case should therefore be defined where all other cases can be evaluated. By means of this reference case and assuming that all unknown or undetailed medical phenomena are the same in all rooms considered, a relative risk of infection can be determined instead of the absolute risk of infection, which cannot be quantified exactly.
In the following, the average living situation is considered as the reference environment in this context, whereby each inhabitant of a household can be infected like the population of all persons in Germany. Thus, the transmission of a virus through aerosols in a room can be compared with the probability of infection in an average apartment. In principle, any reference can be selected at this point. The values of the relative risk always refer to the selected reference case.
For a typical apartment, the relevant volume flow rate can be calculated by equation (8) as the product of the floor area Aref, the clear room height href and the air exchange rate LWref.
| (8) |
This results in the air exchange rate LW generally as the quotient of air volume flow and room volume:
| (9) |
The floor space assumed in Table 1 for the reference apartment corresponds to the average living space for households in Germany according to the supplementary program "Living in Germany" of the 2018 Microcensus, whereby two persons present can be assumed with approximately 46 m² per capita (Statistical Offices of the Federal Government and the States 2019). For living spaces, it is assumed that the entire room air is exchanged every two hours. Together with a stay of 8 h, which was chosen analogous to a typical working day, the reference scenario can thus be regarded as a day at the weekend or a working day in the home office. To calculate the probability of encountering a person who is infected, 83 million inhabitants and, at the beginning of August 2020, about 10,000 currently infected persons are assumed for Germany, which is calculated from the number of all registered cases minus those already recovered and deceased (Robert Koch Institute 2020b). The number of people actually infected is often estimated to be many times higher.
Table 1. Assumptions for the reference environment of a typical apartment.
| Parameter | Value |
Floor space in m² | Aref | 93 |
Room height in m | href | 2.4 |
Air exchange in 1/h | LWref | 0.5 |
Number of persons present | nR,ref | 2 |
Length of stay in h | τref | 8 |
Likelihood of encountering at least one infected person | PKPR,ref | 0.00024 |
If equation (7) is now used for any scenario to be evaluated ARInfand for the reference scenario of a typical apartment ARInf,ref, the relative risk of infectionRRInfcan be calculated according to equation (10).
| (10) |
Used as follows:
|
|
| (11) |
|
|
This relative risk assessment allows the general infection parameter κInf, which cannot be quantified according to the current state of knowledge, to be removed from the equation, assuming for simplicity that it is the same in all considered environments and for all persons. Furthermore, assuming that persons with the same physiological characteristics are present in both environments, both the exhaled aerosol quantity ṅAerosolas well as the respiratory volume flow V̇A can be shortened. Remaining variables in the equation are exclusively technical parameters of the room, the room occupancy, and the statistical variables describing the current course of infection.
In order to evaluate the relative risk of infection compared to a stay in one’s own living environment, boundary conditions for different ventilated comparison environments are defined below. Unless otherwise stated, the volume of air in the room refers to the clear internal dimensions without taking into account furniture or other fixtures.
No breaks or interruptions are taken into account in the times of stay. At this point it should be noted that the design values for air exchange rates given in standards and guidelines often do not correspond to the actual conditions. All values for air exchange rates, retention times, and occupancy rates given here are not to be understood as generally valid for the respective room types, but rather as examples for the assumed example.
The assumptions for the comparative measurements in the Table 2 are as follows: A single-family house with a similar room height, hygienic air exchange, and length of stay as the reference apartment is assumed as a further residential building. Together with a floor space of 140 m², this results in a volume of approximately 336 m³, which is assumed here for simplicity as an air compound. In order to be able to consider situations with several house guests, occupancy rates of up to 20 persons are considered in the following.
The reference values for a classroom for an exemplary school day are based on a field study on air quality and acoustics in schools carried out by Heinz Trox Wissenschafts gGmbH in the spring and summer of 2019. The evaluation of the recorded room geometries results in an average floor area of 64 m² with an average clear height of 3.27 m, a room volume of about 210 m³, and an average of 27 seats. The mechanical ventilation units recorded within the scope of the field study had nominal volume flows of up to 850 m³/h, which, however, could not be operated with the highest fan speed due to the increased flow noise during lessons. Accordingly, air exchange rates below 4/h can be assumed to be realistic.
An office environment with an average 40-hour week is considered as representative of a typical workplace. Based on the Technical Rules for Workplaces ASR A1.2, which concretize the workplace guidelines, 8 m² floor space per workstation is assumed. For a multi-person office with four workstations, a conservative estimate results in a floor space of 26 m² and a room volume of 65 m³, while maintaining the minimum permissible clear room height of 2.75 m for this floor space. Open-plan offices with a floor space of 400 m² or more and a clear height of at least 3 m are still considered open-plan offices, resulting in a minimum room volume of 1,200 m³. Together with a minimum space requirement of 12 m² per workstation, this results in a maximum occupation of 33 persons. (Federal Institute for Occupational Safety and Health (BAuA) 2013).
A lecture hall and an exhibition hall will be used as additional non-residential buildings. For an exemplary large lecture hall with seating for about 1,000 people, a floor space of 935 m² and a volume of about 10,000 m³ is assumed. For lecture halls at RWTH Aachen University, typically 3 to 3.5 air changes per hour are set.
With an exhibition hall, an environment with a very large spatial volume is still considered. The assumed comparative environment is based on a large hall of the Frankfurt Fair. With side lengths of around 75 and 160 m and an average clear height of around 13 m, the result is a gross floor area of 12,000 m² and an air volume of around 156,000 m³. The specified air exchanges were taken from the current "Protection and Hygiene Concept for the Organization of Trade Fairs and Congresses on the Exhibition Grounds of Messe Frankfurt (Status 18.05.2020)". With the floor space of 3 m² per person or ticket sold, as provided for by current regulations, the maximum occupancy of the hall is 4,000 persons.
Table 2. Assumptions and typical boundary conditions for comparison environments.
|
| Single family house | Classroom | Multi-person office | Open-plan office | Lecture Hall (large) | Exhibition hall (large) |
V | m³ | 390 | 210 | 65 | 1200 | 10.000 | 138.000 |
LW | 1/h | 0,5 | to 4 | to 4 | to 4 | up to 3,5 | 2 ... 5 |
nR,max | – | 20 | 35 | 4 | 33 | 1000 | 4000 |
τ | h | 8 | 5 | 8 | 8 | 1,5 | 2.5 |
In the following, the infection risk is graphically represented for the different rooms under variable boundary conditions relative to the apartment assumed as the reference environment. In the diagrams below, the number of persons is plotted above the air exchange rate, with the relative risk of infection shown in color according to a traffic light extended by the color orange. To allow comparison of different scenarios by color, the same air exchange and risk axes were chosen for all immobile environments in Figure 2. Yellow corresponds to a double, and red to at least six times the relative risk of infection. The lines superimposed on the color gradients indicate the limits of half, equal and double the risk of infection compared to the reference environment for easier orientation. It is to be pointed out again that the visualizations, which represent calculated values based on all simplifications mentioned throughequation (11), apply in each case only to the exemplarily accepted space volumes and durations of stay. The influence of latter-mentioned sizes is not dealt with further here.
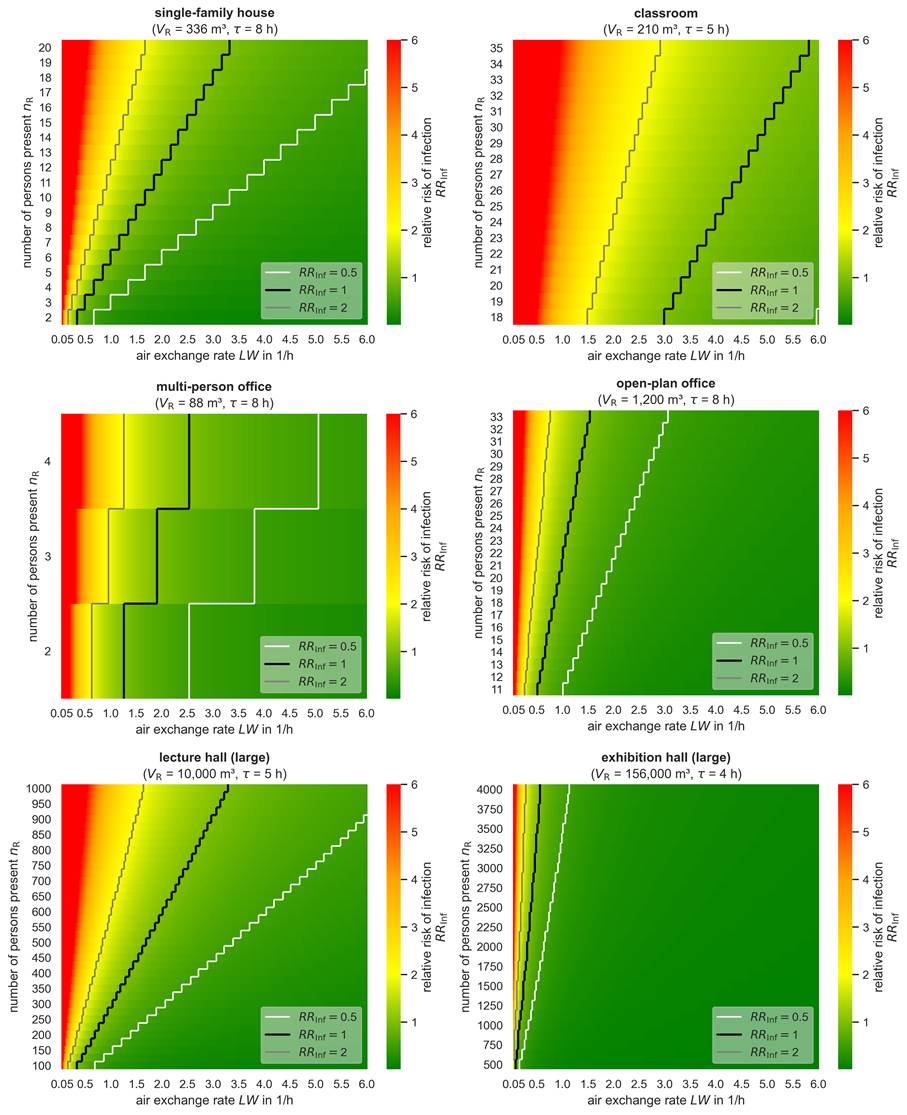
Figure 2. Relative risk of infection by aerosols in different immobile comparison environments compared to the reference apartment.
In the case of a single-family house, a family of four persons is assumed at first, whereby the relative risk of infection is already indicated from two persons upwards, analogous to the assumed occupation of the reference apartment. With an assumed air exchange rate of 0.5/h, the risk of infection is already one third higher for four persons than in the case of the reference apartment: While both persons have about 46 m² floor space and 110 m³ air volume each in the first-mentioned environment, 35 m² and 84 m³ per capita remain in the considered single-family house. If 20 persons are present for a family celebration or on a comparable occasion, the relative risk of infection is about 6.6 with unchanged ventilation habits. 3.3 air changes per hour would be necessary for a relative risk of 1. It should be pointed out that the assumption made here of an air network in the entire building is not unrestricted in reality, so that locally higher infection risks can occur within the building.
Classrooms are particularly critical because of their sometimes high-occupancy rates and long operation times. If half an air exchange per hour is also assumed, which is quite realistic under unfavorable outside conditions and insufficiently used window ventilation, the assumed maximum occupation with 35 persons present would result in an almost 12-fold higher risk of infection than in the reference environment. Even with a very low occupancy of 18 persons, a relative risk of 1 would still require about three times the air exchange rate per hour and thus a volume flow of 630 m³/h. A volume flow of this magnitude can only be provided all year round by a ventilation system. The flow noise caused must be so low that the learning environment is not negatively affected. Pure window ventilation will not be able to provide sufficient air exchange, especially in winter and in noisy outdoor environments.
When comparing the office spaces, the significantly more spacious traffic areas for open-plan offices in the ASR A1.2 become apparent. Whereas in a multi-person office with four full occupants, a relative risk of 1 requires about 2.5 air changes per hour, in an open-plan office about 1.5 air changes per hour would be sufficient even with the assumed full occupancy of 33 people. The minimum number of persons considered in the diagram is 11 persons, which is one third of the maximum number of persons.
In the case of the large lecture hall, a 3.3-fold air exchange per hour is sufficient to achieve a relative risk of infection of 1 when fully occupied. Also, lower occupancy densities with one tenth of the maximum occupancy are shown in order to be able to consider a typical examination situation or less numerously attended events. In the case of the exhibition hall, the risk of infection at typical air exchange rates - even at maximum occupancy - is significantly lower than the risk in the domestic reference environment. In contrast to the room types presented so far, these event rooms require much larger room volumes anyway in order to ensure a sufficiently large smoke-free layer in case of fire, for example. Although the area-related person density is not dissimilar to that of a classroom, each person has a significantly larger vertical column of air at his or her disposal. It should be noted here that stand structures can significantly reduce the traffic area compared to the gross floor area.
Particularly in large rooms, it must be taken into account that the assumption made here of ideal mixed ventilation must be critically questioned. A complete dilution of the polluted aerosols is not always to be expected, so that locally higher concentrations of aerosols can occur. However, in this first analysis the storage capacity of the room volume is also neglected, although for an air exchange rate of 3/h, which can be assumed to be realistic in case of a trade fair, the space-time constant is 20 minutes. Consequently, the stationary values assumed here would only be reached after one hour and forty minutes (corresponding to 5·τn). In order to clarify the concentration distribution in larger rooms, measurements are planned by the Heinz Trox Foundation in the autumn of this year.
In this paper, an approach was developed to calculate a relative risk of infection by virus transport via aerosols in different rooms and uses compared to an apartment as a reference environment. Based on the current ratio of COVID-19 infected persons and the total population in Germany, the probability of an infected person being present in the room was modelled for the respective room occupancy. With this probability and based on room-specific parameters and a hypothetical rate of infectious aerosol particles released into the room air by an infected person, a model for the equilibrium concentration of infectious aerosol particles in the room air was established.
The results show that with sufficiently high air exchange rates in all comparison environments, a relative risk of infection by aerosols smaller than 1 can be achieved. The risk of infection from contaminated aerosols is lower in this case than in the reference environment of a typical apartment. Even if this value does not indicate absolute safety, this reference allows a consideration of further protective measures. However, it is also clear that without adequate ventilation of the rooms, the risk of infection is very high.
In classrooms, this analysis shows that, given the high occupancy rates and length of stay, high air exchange rates are required to maintain relative risk of infection in the area at 1. In the short term, at least oneCO₂ traffic light should be used in practice as an indicator of the amount of outside air for each person. For all new schools and renovation measures, the installation of a sufficiently dimensioned ventilation system is urgently recommended. In rooms with a larger room volume such as open-plan offices, lecture halls and exhibition halls, there is a relative risk of infection of less than 1 even for comparatively low air exchange rates, since the person-related air volumes are very high due to the large room air volumes. Additional storage or buffering effects, which become more significant with increasing room heights, were not considered in this analysis.
In conclusion, it should be emphasized that the method presented in this paper allows for the analysis of relative risks and thus provides a comparative perspective to the public discourse, which often focuses on absolute risk and collateral.
For more detailed considerations the calculation model has to be modified accordingly in a next step. The following aspects could be included in future considerations, which extend the scope of the presented model.
In the previous considerations, it was assumed that the persons in the reference household and the comparison environment to be considered came from the same population. In order to take local hotspots or sources of infection into account, different numbers of infected persons and different sizes of populations can be assumed for the reference and comparison environment.
In the context of this paper, it was assumed for simplicity's sake that the respiratory volume flows in the reference and comparison environments did not differ from each other, which meant that they cancelled each other out and did not have to be further considered. Thus, by considering different respiratory flow rates, different activity levels and workloads could be approximated. Furthermore, new findings on the production rate of aerosols contaminated with viruses can be included in this analysis, taking into account different metabolic rates.
Furthermore, different speech fractions and volumes should be considered by differentiating the exhaled aerosol volumes between the reference and comparison environments, since significant differences in the respective aerosol exposure are to be expected between still and quiet work in a library, a visit to the cinema or work in a call center. The increased release of aerosols as a result of certain respiratory activities could already be demonstrated in the context of a choir rehearsal (Hamner et al. 2020). In this context, investigations by Asadi et al. could be used (Asadi et al. 2019).
Depending on the airflow and temperature conditions used, there can be considerable differences in the aerosol concentration in a room. Thereby local effects in real mixed ventilation systems like stagnation and short-circuit flows have to be addressed and evaluated. Additionally, the effect of a source air flow on the aerosol dispersion can be considered. The natural uplift flow of the supply air introduced near the ground with low temperature and low momentum transports the contaminated breathing air from the occupied zone directly upwards and towards the ceiling near extraction. This enables a better air quality near the floor. In addition, the influence of air filtering and the effectiveness of additional cleaning methods such as the use of UVC sources should be investigated in connection with mechanical ventilation.
Finally, the transient effects of indoor air flows, especially in large rooms, can be discussed. Here, the storage capacity of the available room volume can be considered, which especially influences the evaluation of rooms with temporary use. In addition, the investigation of natural ventilation scenarios with cross-ventilation and impulse ventilation is of great importance, since most buildings in Germany do not have a mechanical ventilation system.
The contribution was financially supported by the Heinz Trox Foundation.
2019 ASHRAE Handbook. Heating, Ventilating, and Air-Conditioning Applications (2019). Atlanta, GA: ASHRAE.
Asadi, Sima; Wexler, Anthony S.; Cappa, Christopher D.; Barreda, Santiago; Bouvier, Nicole M.; Ristenpart, William D. (2019): Aerosol emission and superemission during human speech increase with voice loudness. In: Scientific reports 9 (1). DOI: 10.1038/s41598-019-38808-z.
Azimi, Parham; Stephens, Brent (2013): HVAC filtration for controlling infectious airborne disease transmission in indoor environments: Predicting risk reductions and operational costs. In: Building and Environment 70, S. 150-160. DOI: 10.1016/j.buildenv.2013.08.025.
Federal Institute for Occupational Safety and Health (BAuA) (Ed.) (2013): ASR A1.2, Room dimensions and movement areas. Available online at https://www.baua.de/DE/Angebote/Rechtstexte-und-Technische-Regeln/Regelwerk/ASR/pdf/ASR-A1-2.pdf, last updated May 2018, last checked 03.08.2020.
Buonanno, G.; Stabile, L.; Morawska, L. (2020): Estimation of airborne viral emission: Quanta emission rate of SARS-CoV-2 for infection risk assessment. In: Environment international 141. DOI: 10.1016/j.envint.2020.105794.
Chan, K. H.; Peiris, J. S. Malik; Lam, S. Y.; Poon, L. L. M.; Yuen, K. Y.; Seto, W. H. (2011): The Effects of Temperature and Relative Humidity on the Viability of the SARS Coronavirus. In: Advances in virology 2011. DOI: 10.1155/2011/734690.
Consileon Business Consultancy GmbH (Ed.) (2020): Coronavirus risk calculator. Available online at https://covid-o-mat.de/, last checked on 03.08.2020.
Dai, Hui; Zhao, Bin (2020): Association of infected probability of COVID-19 with ventilation rates in confined spaces: a Wells-Riley equation based investigation.
Deutsche Lufthansa AG (Ed.): Airbus A320-200. Available online at https://www.lufthansa.com/de/de/320, last checked on 03.08.2020.
Duguid, J. P. (1946): The size and the duration of air-carriage of respiratory droplets and droplet-nuclei. In: The Journal of Hygiene 44 (6), S. 471-479. DOI: 10.1017/S0022172400019288.
Fears, Alyssa C.; Klimstra, William B.; Duprex, Paul; Hartman, Amy; Weaver, Scott C.; Plante, Kenneth S. et al. (2020): Persistence of Severe Acute Respiratory Syndrome Coronavirus 2 in Aerosol Suspensions. In: Emerging infectious diseases 26 (9). DOI: 10.3201/eid2609.201806.
Fineberg, Harvey V. (2020): Rapid Expert Consultation on the Possibility of Bioaerosol Spread of SARS-CoV-2 for the COVID-19 Pandemic (April 1, 2020). Washington, D.C.: National Academies Press.
Großmann, Holger (2013): Car air conditioning. Berlin, Heidelberg: Springer Berlin Heidelberg.
Guenther, Thomas; Czech-Sioli, Manja; Indenbirken, Daniela; Robitailles, Alexis; Tenhaken, Peter; Exner, Martin et al. (2020): Investigation of a superspreading event preceding the largest meat processing plant-related SARS-Coronavirus 2 outbreak in Germany. In: SSRN Journal. DOI: 10.2139/ssrn.3654517.
Hamner, Lea; Dubbel, Polly; Capron, Ian; Ross, Andy; Jordan, Amber; Lee, Jaxon et al. (2020): High SARS-CoV-2 Attack Rate Following Exposure at a Choir Practice - Skagit County, Washington, March 2020. In: MMWR. Morbidity and mortality weekly report 69 (19), S. 606-610. DOI: 10.15585/mmwr.mm6919e6.
Han, Z. Y.; Weng, W. G.; Huang, Q. Y. (2013): Characterizations of particle size distribution of the droplets exhaled by sneeze. In: Journal of the Royal Society, Interface 10 (88). DOI: 10.1098/rsif.2013.0560.
Lai, Ka man; Nasir, Zaheer Ahmad; Taylor, Jonathon (2013): Bioaerosols and Hospital Infections. In: Ian Colbeck und Mihalis Lazaridis (Hg.): Aerosol Science. Chichester, UK: John Wiley & Sons, Ltd, S. 271-289.
Li, Yuguo; Qian, Hua; Hang, Jian; Chen, Xuguang; Hong, Ling; Liang, Peng et al. (2020): Evidence for probable aerosol transmission of SARS-CoV-2 in a poorly ventilated restaurant.
Morawska, Lidia; Cao, Junji (2020): Airborne transmission of SARS-CoV-2: The world should face the reality. In: Environment international 139. DOI: 10.1016/j.envint.2020.105730.
Mundt, Elisabeth (Hg.) (2004): Ventilation effectiveness. Brussels: Rehva (REHVA Guidebook, 2).
Neumann, Hans-Dieter; Buxtrup, Martin (2014): Healthy air in schools - Part 2: Assessment of CO2 concentration and thermal comfort in classrooms. Edited by Unfallkasse Nordrhein-Westfalen. Düsseldorf (Prevention in NRW, 57). Available online at https://www.unfallkasse-nrw.de/fileadmin/server/download/praevention_in_nrw/PIN_57_Gesunde_Luft_in_Schulen_II.pdf, last checked on 03.08.2020.
Ott, Wayne; Klepeis, Neil; Switzer, Paul (2008): Air change rates of motor vehicles and in-vehicle pollutant concentrations from secondhand smoke. In: Journal of exposure science & environmental epidemiology18 (3), S. 312-325. DOI: 10.1038/sj.jes.7500601.
Pan, M.; Lednicky, J. A.; Wu, C-Y (2019): Collection, particle sizing and detection of airborne viruses. In: Journal of applied microbiology 127 (6), S. 1596-1611. DOI: 10.1111/jam.14278.
Papineni, R. S.; Rosenthal, F. S. (1997): The size distribution of droplets in the exhaled breath of healthy human subjects. In: Journal of aerosol medicine: the official journal of the International Society for Aerosols in Medicine 10 (2), S. 105-116. DOI: 10.1089/jam.1997.10.105.
Riley, E. C.; Murphy, G.; Riley, R. L. (1978): Airborne spread of measles in a suburban elementary school. In: American journal of epidemiology 107 (5), S. 421-432. DOI: 10.1093/oxfordjournals.aje.a112560.
Robert Koch-Institute (Ed.) (2020a): Answers to frequently asked questions about the coronavirus SARS-CoV-2 / disease COVID-19. Available online at https://www.rki.de/SharedDocs/FAQ/NCOV2019/gesamt.html, last updated on 03.07.2020, last reviewed on 07.08.2020.
Robert Koch Institute (Ed.) (2020b): COVID-19: Case numbers in Germany and worldwide. Available online at https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Fallzahlen.html, last updated on 08/03/2010, last checked on 08/03/2010.
Santarpia, Joshua L.; Rivera, Danielle N.; Herrera, Vicki; Morwitzer, M. Jane; Creager, Hannah; Santarpia, George W. et al. (2020): Aerosol and Surface Transmission Potential of SARS-CoV-2.
Smither, Sophie J.; Eastaugh, Lin S.; Findlay, James S.; Lever, Mark S. (2020): Experimental aerosol survival of SARS-CoV-2 in artificial saliva and tissue culture media at medium and high humidity. In: Emerging microbes & infections 9 (1), S. 1415-1417. DOI: 10.1080/22221751.2020.1777906.
Somsen, G. Aernout; van Rijn, Cees; Kooij, Stefan; Bem, Reinout A.; Bonn, Daniel (2020): Small droplet aerosols in poorly ventilated spaces and SARS-CoV-2 transmission. In: The Lancet Respiratory Medicine 8 (7), S. 658-659. DOI: 10.1016/S2213-2600(20)30245-9.
Stansted News Limited (Ed.): Airbus ACJ320. Business Air News magazine. Available online at https://www.businessairnews.com/hb_aircraftpage.html?recnum=ACJ320, last checked 03.08.2020.
Statistical Offices of the Federal and State Governments (Ed.) (2019): Housing in Germany. Supplementary program of the microcensus 2018. Federal Statistical Office. Available online at https://www.destatis.de/DE/Themen/Gesellschaft-Umwelt/Wohnen/Publikationen/Downloads-Wohnen/wohnen-in-deutschland-5122125189005.html, last checked on 03.08.2020.
Sun, Chanjuan; Zhai, Zhiqiang (2020): The efficacy of social distance and ventilation effectiveness in preventing COVID-19 transmission. In: Sustainable Cities and Society 62. DOI: 10.1016/j.scs.2020.102390.
Tabarrok, Alex (2020): COVID-19 Event Risk Assessment Planner. Ed. by Marginal Revolution. Available online at https://marginalrevolution.com/marginalrevolution/2020/03/covid-19-event-risk-assessment-planner.html, last reviewed on 03.08.2020.
van Doremalen, Neeltje; Bushmaker, Trenton; Morris, Dylan H.; Holbrook, Myndi G.; Gamble, Amandine; Williamson, Brandi N. et al. (2020): Aerosol and Surface Stability of SARS-CoV-2 as Compared with SARS-CoV-1. In: The New England journal of medicine 382 (16), S. 1564-1567. DOI: 10.1056/NEJMc2004973.
Wells, William Firth (1934): On Air-Borne Infection*. In: American journal of epidemiology 20 (3), S. 611-618. DOI: 10.1093/oxfordjournals.aje.a118097.
World Health Organization (2014): Infection prevention and control of epidemic- and pandemic-prone acute respiratory infections in health care health care. WHO Guidelines. Geneva: Pandemic and Epidemic Diseases, World Health Organization.
World Health Organization (2020): Transmission of SARS-CoV-2: implications for infection prevention precautions. WHO Guidelines. World Health Organization. Geneva. Online verfügbar unter https://www.who.int/publications/i/item/modes-of-transmission-of-virus-causing-covid-19-implications-for-ipc-precaution-recommendations, zuletzt geprüft am 28.07.2020.
Xie, X.; Li, Y.; Chwang, A. T. Y.; Ho, P. L.; Seto, W. H. (2007): How far droplets can move in indoor environments--revisiting the Wells evaporation-falling curve. In: Indoor air 17 (3), S. 211-225. DOI: 10.1111/j.1600-0668.2007.00469.x.
Yu, Ignatius T. S.; Li, Yuguo; Wong, Tze Wai; Tam, Wilson; Chan, Andy T.; Lee, Joseph H. W. et al. (2004): Evidence of airborne transmission of the severe acute respiratory syndrome virus. In: The New England journal of medicine 350 (17), S. 1731-1739. DOI: 10.1056/NEJMoa032867.
Follow us on social media accounts to stay up to date with REHVA actualities
0