Stay Informed
Follow us on social media accounts to stay up to date with REHVA actualities
|
|
|
R. Gritzki | C. Felsmann | M. Rösler |
TU Dresden | TU Dresden | TU Dresden |
|
|
|
|
|
|
A. Gritzki | M. Iivonen | J. Naumann |
BAuA, formerly TU Dresden | Purmo Group | GWT-TUD, Dresden |
In Part 1 it has been shown, that under EN 442 standard conditions the heat outputs of the simulated radiators were in all cases in very good accordance to the design data in the data sheets.
However, it also became apparent that in case of radiator type 22, for all supply temperature levels and already in the range of typical mass flow rates simulations such as measurements show higher heat outputs (up to approx. 10%) than calculated by the exponential approach according to EN 442-2.
On the other hand, the simulated heat output of radiator types without additional convection plates are for a wide range of flow rates in good accordance to the heat output values based on the exponential calculation approach using the logarithmic over-temperature (again called “exponential approach” in the following). Only at very low mass flow rates the actual heat output is lower compared to the exponential approach. This is also in accordance with the theory found in the literature. For typical fields of application, the exponential approach fits very well.
Detailed investigations bring forth that, if convection plates are present the external heat transfer coefficients decrease with increasing mass flow rates and thus decreasing temperature spreads. In this case, the vertical temperature distribution of the water within the radiator is different from that of the radiator surface and is therefore no longer representative for the external heat transfer. The stronger cool down of the lower parts of the convection plates leads in total to a lower external heat transfer than in case of big temperature spreads.
For this case the application of an extended calculation approach, based on EN 442-2, is introduced to take into account the vertical temperature distribution of the radiator surface. For the examined radiator models with convection plates this calculation approach leads to a significantly improved agreement of the calculated heat outputs with the data based on the numerical simulations.
Symbols | ||
k | heat transfer coefficient | in W/(m² K) |
Km | radiator model constant | – |
∆Tm, ∆Tar | over-temperature (logarithmic or arithmetic) | in K |
ṁ | mass flow rate | in kg/h |
Q̇ | heat output | in W |
Φ | heat output (EN 442-2) | in W |
Tin | supply temperature | in°C |
Tout | return temperature | in°C |
Tr | room air temperature (control point) | in°C |
cp | specific heat capacity | in J/(kg K) |
∆T | difference supply – return temperature | in K |
Indices | |
N | nominal point / design point |
ar | arithmetic |
ln | logarithmic |
50 | design point (at 50 K over-temperature, EN 442-2) |
From Part 1 [1] we have learned that the EN 442-2 [2] approach used to adjust the heat output of radiators to specific temperature conditions lead to some deviation of about 10% compared to both real and virtual radiator performance test results. It has been shown that this uncertainty of the conventional exponential approach is somehow related to radiators with convection plates (type 22) and mainly occurs in case of low mass flow rates, see Figure 1.
In Figure 1 the heating power of two panel radiators with convection plates gained in high performing virtual experiments and the corresponding mass flow rates are displayed as a function of the difference between supply and return temperature (the temperature spread). The heat output under standardized reference conditions (75-65-20) is highlighted. In addition, the diagrams also show the heat output of the radiators at different operating temperature. The adjustment of heating power was done by the EN 442 exponential approach either by using the logarithmic over-temperature ΔTln or the arithmetic over-temperature ΔTar. Logarithmic over temperature is more accurate for heating power prediction but as already discussed lead to some uncertainty as well.
Looking at these results the question arises, what the mismatch causes. First assumption is, that it could be a result of the inhomogeneity of the temperature distributions (see the temperature stratification graphs in Part 1) at the entire radiator surface caused by large temperature spreads. Detailed additional investigations (based on the same logarithmic over-temperature and greatly varying temperature spreads) showed that indeed there is a difference in the vertical temperature distribution of the different radiator parts, see Figure 2. The diagrams show the surface temperatures that have been averaged along small horizontal slices for the entire radiator and for the radiator components (water, radiator shell, convection plates). The radiator surface consists of the radiator metal itself and the convection plates.
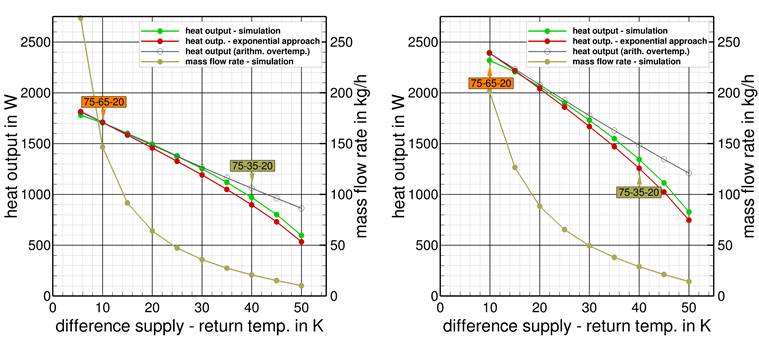
Figure 1. Simulated (green) and catalogue heat output data based on exponential approach (red/gray) at constant supply temp. of 75°C and changed mass flow rates, panel radiators with convection plates, type 22 – left: 1.0 m length, right: 1.4 m length.
![]()
![]()
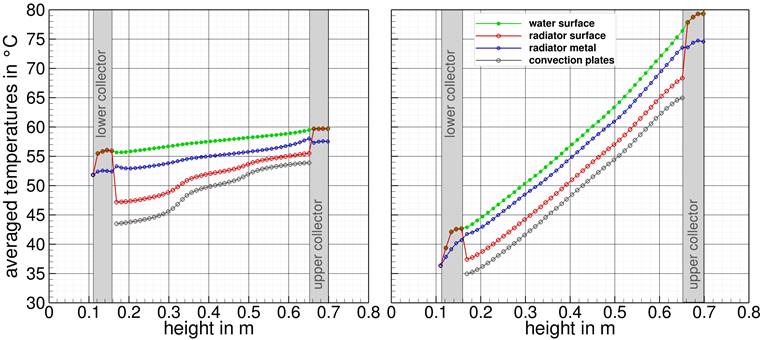
Figure 2. Averaged temperatures based on horizontal slices for different mass flow rates but the same logarithmic over-temperature of 38,2 °C, panel radiator with convection plates, type 22, 1.0 m length – left (a): 256 kg/h, right (b): 28 kg/h.
In case of the large temperature spread (Figure 2b) caused by low mass flow rate, the temperature gradient above the radiator height is quite similar in all parts of the radiator (water, radiator metal and convection plates; the radiator surface reported is a combination of metal and convection plates). So, the averaged radiator temperature follows the water temperature and the vertical temperature distribution of the water is representative for the external heat transfer. So, it is obvious that once the logarithmic over temperature is calculated just based on supply and return water temperatures the radiator surface temperature can be concluded without knowing the exact temperature distribution.
Unfortunately, there is a slightly different situation in the case of small temperature spread (Figure 2a) caused by a high water mass flow rate. The temperature of the convection plates drops much faster from the upper part of the radiator to the lower part than the temperature of the water. Subsequently the vertical temperature distribution of the water is different from that in the whole radiator surface. Keep in mind, that the logarithmic over temperature in EN 442 calculated just from the water temperature entering and leaving the radiator cannot account for these phenomena!
Beside we can argue with heat transfer theory that the external heat transfer coefficients of the radiator decrease if the vertical stratification of temperature becomes lower due to high mass flow rates. Considering this, two effects caused by low mass flow and thus large temperature spreads have been isolated:
1. The logarithmic over temperature is not representing the temperature distribution on the radiator’s heat emitting surface including convection plates.
2. The less stratified vertical temperature profile on the radiator surface in case of high mass flow rates has a limiting impact on the heat transfer coefficient. Heat transfer mechanism is accelerated if there is a significant temperature stratification.
It has to be mentioned that EN 442 standardized testing conditions are characterized by a low temperature spread of 75°C – 65°C=10 K, i.e. radiator model parameter Km and n are estimated for a more unfavourable operation in terms of heat transfer.
To also ensure, as a next step, that the exponential approach based on the logarithmic over-temperature is valid for arbitrary mass flow rates (provided that load-dependent radiator model parameters are known), some additional investigations with constant mass flow rates and varying supply temperatures were done. As an example of this Figure 3 shows the heat output data based on the exponential approach (Km and n always adapted to the respective mass flow) as well as based on the simulations for the panel radiator type 22 (1.4 m) and for two different base mass flow rates. The results clearly show that the adapted exponential approach for all supply temperatures is in very good accordance to the simulated heat output. This also confirms the findings in the literature [3].
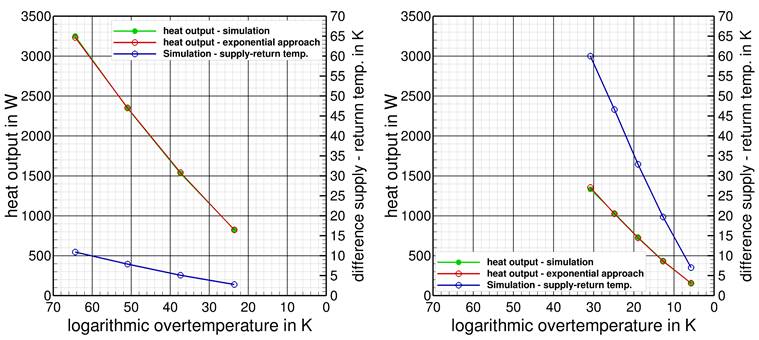
Figure 3. Simulated (green) and heat output data based on exponential approach (orange) at constant mass flow rate and different supply temperatures, panel radiator with convection plates, type 22, 1.4 m – mass flow rate left: 250 kg/h, right: 15 kg/h.
In Figure 4 and in Figure 6 the heat output data and the mass flow rates of the other four radiators without convection plates in dependence on the difference between the supply and the return temperature are displayed for the simulations as well as for the catalogue data based on the logarithmic over-temperature (and based on ΔTar). It is obvious that catalogue data (i.e. the exponential approach) and the simulations fit much better and that in these cases the differences are much smaller. Only at very low mass flow rates the simulated heat output values are slightly lower than the values based on the exponential approach.
The detailed investigations based on the same logarithmic over-temperature and greatly varying temperature spreads showed in this case that the vertical temperature distribution of the water and the entire radiator surface are practically identical, see Figure 5. That means, the vertical temperature distribution of the water is representative for the external heat transfer and in both cases the same values of km and n can be used to predict the heat output.
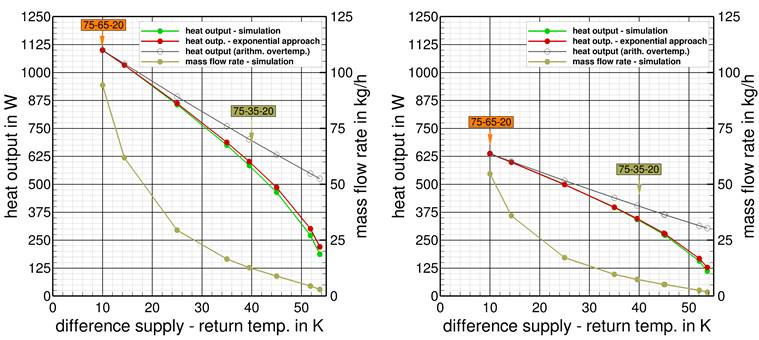
Figure 4. Simulated (green) and catalogue heat output data based on exponential approach (red/gray) at constant supply temperature of 75°C and changed mass flow rates, panel radiators – left type 20, right type 10.
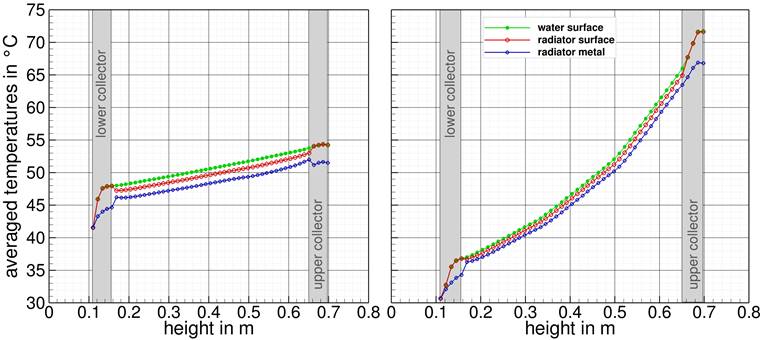
Figure 5. Averaged temperatures based on horizontal slices for different mass flow rates but the same logarithmic over-temperature of 38,2 °C, panel radiator with convection plates, type 20, 1.0 m length – left: 256 kg/h, right: 28 kg/h.
As radiator surface temperature distribution clearly depends also on the presence of convection plates. The results support the presumption that radiator surface temperature distribution and its impact on heat transfer has to be taken into account when looking for a more accurate calculation approach (rather than that already published in EN 442-2), valid also for large temperature differences between supply and return temperature. A new approach is introduced in the next section.
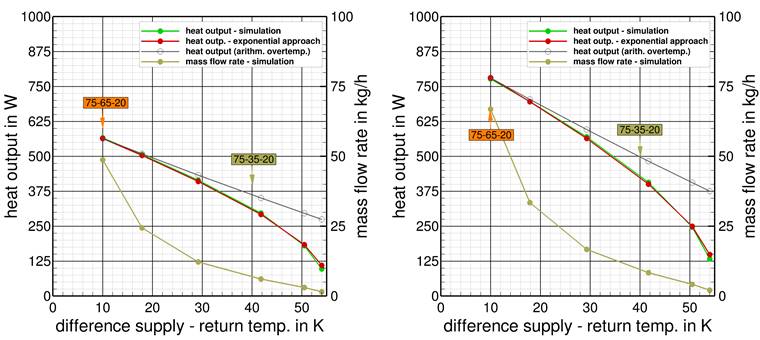
Figure 6. Simulated (green) and catalogue heat output data based on exponential approach (red/gray) at constant supply temperature of 75°C and changed mass flow rates, tubular radiators – left: 2 tubes, right: 3 tubes.
In the previous sections we have explained that the presence of convection plates disturbs the relation between water temperature and surface temperature of the radiator which is one of the basic assumptions for the application of the exponential approach. That means, the original problem occurs, if panel radiators with convection plates are handled as “normal” radiators ignoring the phenomena of heat transfer within the convection plates.
In this section an extended calculation approach for determining the heat output of radiators according to EN 442-2 is presented. The approach is again based on the logarithmic over-temperature ΔTln but is taking into account the new insights derived from numerical simulations of the two radiators with convection plates (type 22). It should be noted that this approach does not solve the original problem, it only circumvents it in order to apply the existing procedure as far as possible.
The theoretical approach for determining the heat transfer coefficient as a function of temperature conditions based on a given nominal point N (design point), described among others by Knabe [4] is
| (4) |
with p = 0.25…0.4 for radiators. Based on this correlation one can determine the heat output of radiators at other operation points by equation
| (5) |
and based on the specifications of the EN 442-2 (constant mass flow, design temperatures of 75-65-20°C, which means 50 K (ΔTln = 49.83 K) over-temperature) it reads
| with |
| and |
| (6) |
Since in the simulations as well as in the measurements both Km and n depend on the temperature spread (which increases with decreasing mass flow rates), it seems reasonable to apply a further correction factor F to the approach according to EN 442-2 which considers both the impact of the temperature spread on the vertical temperature distribution of the radiator surface as well as the non-representative over-temperature calculated just on the water temperature on the external heat transfer. Therefore equation (6) is extended by a factor based on a ratio of the actual temperature spread ΔT = Tin − Tout and the spread at the design point ΔT50 and an radiator model specific exponent q:
| with |
| (7) |
In this approach, which was originally derived on the basis of mass flow ratios, the heat transfer changes only as a function of the radiator temperatures (but we should keep in mind, that in fact effective radiator temperatures are a result of supply water temperature and water mass flow rate). For the two investigated radiators with convection plates (one type, different lengths) the determined values of q are 0.0357 (1.0 m length) and 0.0486 (1.4 m length).
In Figure 7 to Figure 9 the heat output values and the mass flow rates of these two radiator models in dependence on the difference between the supply and the return temperature are displayed for the simulations as well as for the catalogue data based on the extended calculation approach. The consideration of the mass flow induced temperature distribution at the radiator leads to a significant improvement at low mass flow rates and large temperature differences between inlet and outlet. This applies to all temperature levels and both radiator lengths. The relative deviations when using the extended approach for calculating the heat output are in the range of ±1%. Only at very small mass flows below 10% of the design, deviations can be up to ±4%.
Remaining deviations between simulation and calculation are due to inaccuracies of the logarithmic over-temperature, simplifications of the CFD simulation and the neglect of the (weak) temperature dependence of the exponents n and q.
For the extended calculation approach, both exponents n and q can be assumed to be approximately constant for a radiator type, independent of the flow and temperature conditions.
As might be expected, for deviating radiator lengths a relation to determine the exponent q may be found. In the case of the present radiator type, the exponents changed proportionally to the radiator length or the design heat output (“q1.0m” = 0.0357; “q1.4m” = 0.0486):
q1.4 m ≈ (1.4 m / 1.0 m) ∙ q1.0 m
To determine the exponent q und thus the additional factor F, only an additional data set (based on one measurement) with significant deviation from the design mass flow (for example 30 % of the design mass flow rate) is appropriate.
|
|
Figure 7. Simulated (green) and catalogue heat output data based on the extended exponential approach (red) at constant supply temperature of 75°C and changed mass flow rates, panel radiators with convection plates, type 22 – left: 1.0 m length, right: 1.4 m. | |
|
|
Figure 8. Simulated (green) and catalogue heat output data based on the extended exponential approach (red) at constant supply temperature of 55°C and changed mass flow rates, panel radiators with convection plates, type 22 – left: 1.0 m length, right: 1.4 m. | |
|
|
Figure 9. Simulated (green) and catalogue heat output data based on the extended exponential approach (red) at constant supply temperature of 90°C and changed mass flow rates, panel radiators with convection plates, type 22 – left: 1.0 m length, right: 1.4 m. | |
The investigations showed that the EN 442 approach is reliable for a wide range of flow rates to predict the heat output of a radiator with no additional convection plates. Only at very low mass flow rates and thus large temperature drop the exponential approach shows some weakness. Nevertheless, for typical fields of application the exponential approach fits very well, it seems that additional corrections are not necessary.
If convection plates are present, the EN 442 predicts lower higher heat outputs (up to approx. 10%) than either measured by Rettig ICC or virtually tested. This applies to all supply temperature levels already in the range of typical mass flow rates. Detailed investigations showed that the external heat transfer coefficients decrease with decreasing temperature stratification on the radiator surface. Stratification is high for low mass flow rates. In this case the temperature distribution of the water within the radiator is different from that of the radiator surface and is therefore no longer representative for the external heat transfer. In other words, the ratio of the vertical temperature distribution of water and radiator surface is different for different mass flow rates and therefore the radiator model parameters are different as well.
In case of radiators with convection plates, the application of an extended calculation approach to take into account the mass flow-induced change in the external heat transfer coefficient leads to a significantly improved consistency and reliability of the calculated heat outputs. The findings and the suitability of the extended approach should be checked for further radiator models (larger height/length, towel radiators) and connection types as well as the way of determining the additional exponent q in order to ensure their generality. From the practical point of view, it has to be decided if uncertainties of the recent approach justify any effort for improvements. Anyway, the TU Dresden virtual test cabin for radiator testing according to EN 442 is very helpful to analyse heat transfer phenomena at radiators.
[1] Gritzki, R., Felsmann, C., Rösler, M., Gritzki, A., Iivonen, M., Naumann, J. New operating definitions for radiators based on different flow conditions – part 1, Measurements and Simulations, REHVA 2021
[2] EN 442-2. 2014. Radiators and convectors – Part 2. Test methods and rating. Beuth Verlag, Berlin.
[3] H. Bach, D. Schlapmann. 1977. Effektive Übertemperatur zur einheitlichen Darstellung der Wärmeleistung von Raumheizkörpern. Ki 10/77, Teil 6, S. 592-597.
[4] Knabe G. 1992: Gebäudeautomation. Verlag für Bauwesen Berlin, München.
Follow us on social media accounts to stay up to date with REHVA actualities
0